2007COMC加拿大數(shù)學(xué)公開賽真題答案免費(fèi)下載

歷年 Canadian Open Mathematics Challenge加拿大數(shù)學(xué)公開賽

真題與答案下載

翰林國際教育全網(wǎng)首發(fā)

力爭超快速發(fā)布最全資料

助你在升學(xué)路上一帆風(fēng)順

為你

千千萬萬遍

2007 COMC真題答案免費(fèi)下載

共計(jì)2.5小時(shí)考試時(shí)間

此套試卷由兩部分題目組成

Part A共8題，每題5分

Part B共4題，每題10分

共計(jì)12題，滿分80分

不可使用任何計(jì)算器

完整版下載鏈接見文末

部分真題預(yù)覽：

Part A Solutions:

A3)Since AD = 4 and AD is perpendicular to the x-axis, then A has y-coordinate 4. Suppose that the coordinates of A are (a, 4). (This tells us also that D has coordinates (a, 0).)
Since A lies on the line y = x + 10, then 4 = a + 10, or a = ?6.
Therefore, A has coordinates (?6, 4) and D has coordinates (?6, 0).
Since ABCD is a rectangle, then AB is parallel to the x-axis, so B has y-coordinate 4.
Suppose that the coordinates of B are (b, 4). (This tells us also that C has coordinates (b, 0)
since BC is perpendicular to the x-axis.)
Since B lies on the line y = ?2x + 10, then 4 = ?2b + 10 so 2b = 6 or b = 3.
Therefore, B has coordinates (3, 4) and C has coordinates (3, 0).
Now the height of rectangle ABCD equals the length of AD, so is 4.
The width of rectangle ABCD equals the length of CD, which is 3 ? (?6) = 9.
Therefore, the area of rectangle is 9 × 4 = 36.
Answer: 36

Part B Solutions:

B3)

1. Alphonse should win.
   If Alphonse starts by taking 1 stone, then by Rule #3, Beryl must remove at least 1 stone and at most 2(1) ? 1 = 1 stone. In other words, Beryl must remove 1 stone.
   This in turn forces Alphonse to remove 1 stone, and so on.
   Continuing in this way, Alphonse removes 1 stone from an odd-sized pile at each turn and Beryl removes 1 stone from an even-sized pile at each turn. Thus, Alphonse removes the
   last stone.
   Therefore, Alphonse wins by removing 1 stone initially since 7 is odd.
   (In fact, this argument shows that Alphonse should win whenever N is odd.)
2. Beryl should win.
   We make a chart in which the rows enumerate a possible combination of moves. Each move indicates the number of stones removed.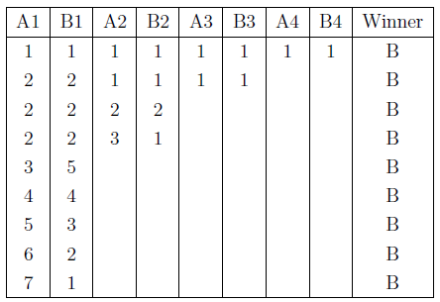
   Thus, no matter what number of stones Alphonse removes initially, there is a move that Beryl can make which allows her to win. (There are possible combinations of moves where Alphonse wins that are not listed in this chart.) Therefore, Beryl should win when N = 8.
   Her strategy is:
   • If Alphonse removes 3 or more stones, then he can remove the remaining stones in the pile and win.
   • If Alphonse removes 1 or 2 stones, then he can win by using the table above, choosing a row for which she wins. In effect, Beryl repeats Alphonse’s move on her first turn. This ensures that Alphonse receives a pile with an even number of stones and that he can remove no more than 3 stones on his next turn. Thus, she can win, as the table shows.
3. Two Solutions:
   1. Solution 1: We show that Beryl has a winning strategy if and only if N = 2^m, with m a positive integer.
      First, if N is odd, we know that Alphonse has a winning strategy as in (a) (Alphonse removes 1 stone, forcing Beryl to remove 1 stone, and so on).
      Second, if N = 2, then Beryl wins as Alphonse must remove 1 stone to begin, so Beryl removes the remaining stone.
      Next, we show that if N = 2k, then the player who has the winning strategy for N = k also has a winning strategy for N = 2k. This will tell us that Beryl has a winning strategy for N = 2, 4, 8, 16, . . . (in general, for N = 2^m) and that Alphonse has a winning strategy if N = 2^mq where q is an odd integer (since Alphonse wins for N = q, 2q, 4q, . . .). Since every even integer can be written in one of these two forms, this will complete our proof.
      So consider N = 2k.
      • If either player removes an odd number of stones from an even-sized pile (leaving an odd-sized pile), then they can be forced to lose, as the other player can then remove 1 stone from an odd-sized pile and force a win as in (a). So if Alphonse removes an even number of stones to start, then Beryl should next remove an even number of stones (so that Alphonse can’t immediately force her to lose), so the pile size will always remain even and each player’s move will always be to remove an even number of stones.
      • Suppose that Alphonse has a winning strategy for N = k of the form a₁, b₁, a₂, b₂, . . . , a_j . Here, we mean that Alphonse removes a1 stones on his first turn and responds to Beryl’s first move b₁ by removing a₂ and so on. (Of course, a₂ will depend on b₁ which could take a number of values, and so on.) Since these are valid moves, then 1 ≤a₁ < k, and b₁ < 2a₁, and a₂ < 2b₁, and so on.
        Then 2a₁, 2b₁, 2a₂, 2b₂, . . . , 2a_j will be a winning strategy for Alphonse for N = 2k since 1 < 2a₁ < 2k, and 2b₁ < 2(2a₁), and 2a₂ < 2(2b₁), and so on, so this is a valid sequence of moves and they exhaust the pile with Alphonse taking the last stone. In other words, to win when N = 2k, Alphonse consults his winning strategy for N = k. He removes twice his initial winning move for N = k. If Beryl removes 2b stones next, Alphonse then removes 2a stones, where a is his winning response to Beryl removing b stones in the N = k game. This guarantees that he will win.
      • Suppose that Beryl has a winning strategy for N = k.
        By an analogous argument, Beryl has a winning strategy for N = 2k, for if Alphonse removes 2a stones, then she removes 2b stones, where b is her winning responding
        move to Alphonse removing a stones in the N = k game.

Therefore, Beryl wins if and only if N = 2m, with m a positive integer.

完整版真題資料可以底部二維碼免費(fèi)領(lǐng)取↓↓↓

[vc_btn title="查看更多COMC加拿大數(shù)學(xué)奧賽相關(guān)詳情" color="primary" align="center" i_icon_fontawesome="fa fa-globe" css_animation="zoomIn" button_block="true" add_icon="true" link="url:http%3A%2F%2Fwww.linstitute.net%2Farchives%2F99767||target:%20_blank|"]