2023HiMCM新賽季報名正式開啟！附HiMCM數模競賽流程解析

當提到廣受影響力的數學學術活動時，許多人會立刻想到AMC、AIME、PUMaC等學術活動，但這些學術活動有一個共同點——都是筆試答題。那么，是否存在一種形式新穎、更具挑戰性的數學學術活動呢？

事實上，確實存在這樣一種學術活動！

HiMCM是一項獨特的數學學術活動，它涉及團隊賽、建模和提交論文。不僅需要選手具備編程技巧，更注重數學、邏輯思維和論文寫作能力。

同時，該學術活動借鑒了美國大學生數學建模學術活動的模式，并結合了中學生的特點進行設計。它是由美國數學及其應用聯合會（COMAP）主辦的一項國際性數學學術活動活動。

2023HiMCM賽事基本信息

適合人群

對應用數學感興趣、并有一定的數學基礎，未來專業為數學、工程、計算機、商科的學生。適合在初三到高三，希望挑戰自我，沖擊世界知名大學的學生。

隊伍人數

由1-4名在校高中生組成，所有隊員必須來自同一所學校，配備一位指導老師。

開放報名

2023年9月29日

注冊截止日期

美國東部時間2023年11月1日星期三下午2:00

比賽窗口打開

美國東部時間2023年11月1日星期三下午3:01

比賽窗口關閉

美國東部標準時間2023年11月14日星期二晚上8:00

解決方案報告截止日期

美國東部標準時間2023年11月14日星期二晚上9:00

比賽結果公布時間

2024年2月1日或之前公布

快來翰林尋找志同道合的伙伴吧！組隊信息可咨詢顧問老師~

數學建模的主要過程

在A First Course in Mathematical Modeling這本教材中出現的數學建模五步法，應該是大家耳熟能詳的，這里給大家分享一下：

Part.1第一步

提出問題

Part.2第二步

選擇建模方法

Part.3第三步

推導模型的公式：

1、?將第一步中得到的問題重新表達成第二步選定的建模方法所需要的形式.

2、?你可能需要將第一步中的-些變量名改成與第二步所用的記號一致.

3、?記下任何補充假設，這些假設是為了使在第一步中描述的問題與第二步中選定的數學結構相適應而做出的。

Part.4第四步

求解模型：

1、?將第二步中所選方法應用于第三步得到的表達式.

2、?注意你的數學推導，檢查是否有錯誤，你的答案是否有意義．

3、?采用適當的技術．計算機代數系統，圖形，數值計算的軟件等都能擴大你能解決問題的范圍，并能減少計算錯誤．

Part.5第五步

回答問題用非技術性的語言將第四步的結果重新表述。

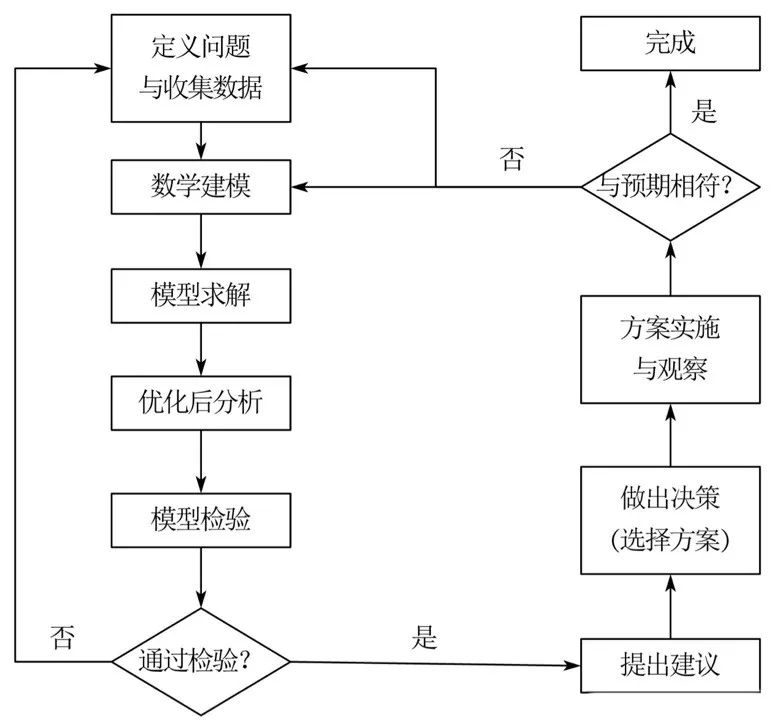
這個流程圖便是基于模型解決問題的一般流程，數學建模五步法與其相比更加精簡，更適合在數學建模學術活動中應用，而該流程在實際生活中也更具指導意義！