數(shù)學(xué)Pure Mathematics Numerical Methods總結(jié)

Numerical Methods中涉及到的畫圖問題。考綱中對這個知識點的描述如下：

 

我們不但要會用這個知識點中涉及到的公式求方程的近似解，還要會畫出圖像來演示能否求出近似解。下面我們通過知識點復(fù)習(xí)和例題講解來具體說明。

Part 1知識點復(fù)習(xí)

Numerical methods 這一章介紹了兩種求方程近似解的方法。第一種是Iteration formula, 即遞推公式。第二種是Newton-Raphson method, 一種特殊的遞推公式。

01Iteration formula

這個方法的整體思路如下：

我們不用考慮g(x)的形式，因為考試時都會給出來x=g(x)的表達(dá)式，我們只需由f(x)=0變形到x=g(x)即可。然后我們可以根據(jù)題中給出的起始值x0,反復(fù)帶入計算器來求出后續(xù)的值，從而得到精確到一定位數(shù)的近似解。

這種方法能否得到方程f(x)=0的近似解（root)取決于x=g(x)的形式。有些變形后的遞推公式能得到近似解，我們稱：The iteration will converge?(收斂）to a root. 有兩種圖形可以展示這個過程，這兩種圖形的畫法需要掌握，很有可能在考試中出現(xiàn)。

第一種是Staircase diagram?即階梯圖。

 

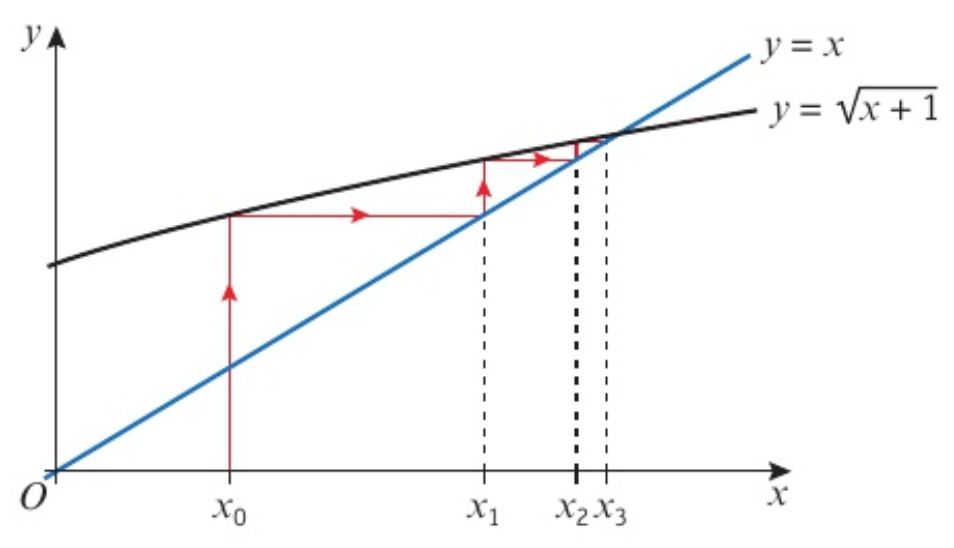
第二種是cobweb diagram 即蛛網(wǎng)圖

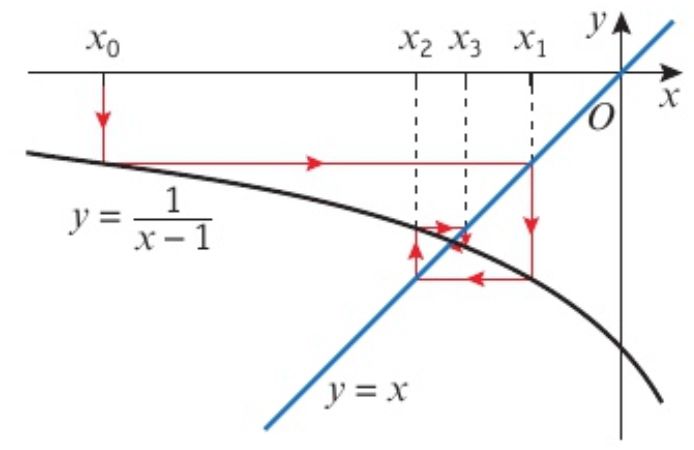
但是有些變形后的公式會使得求出的值越來越遠(yuǎn)離真實根，我們稱：The iteration will diverge?(發(fā)散）.

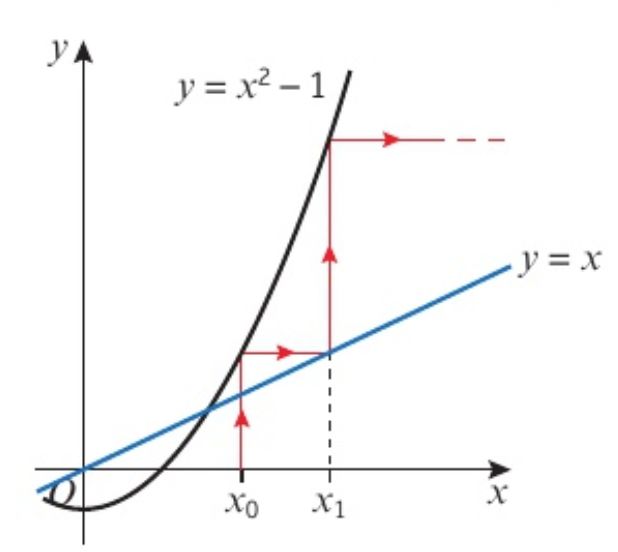
02Newton-Raphson method

這個方法有一個具體的公式，考試的公式表中也會給出來。

這個方法是反復(fù)利用f(x)在某一點的切線與x軸的交點來逐漸逼近方程分f(x)=0的根。如下圖所示：

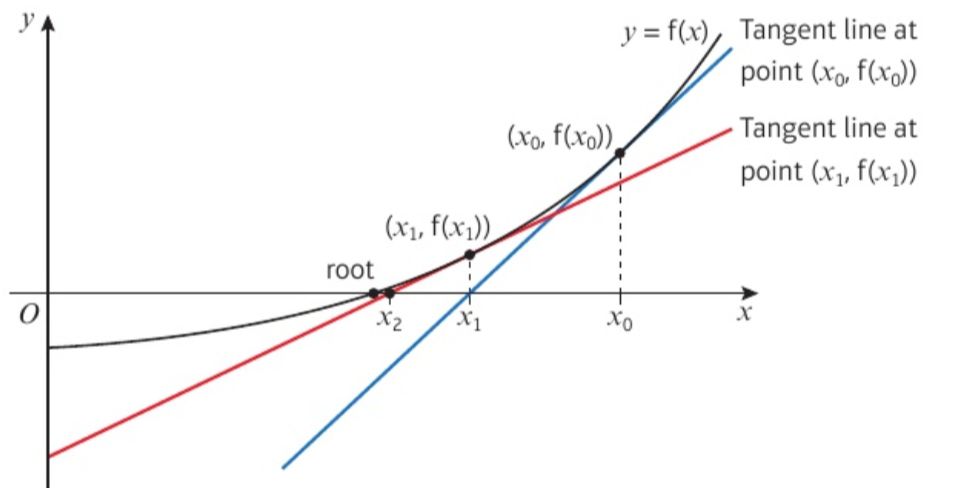
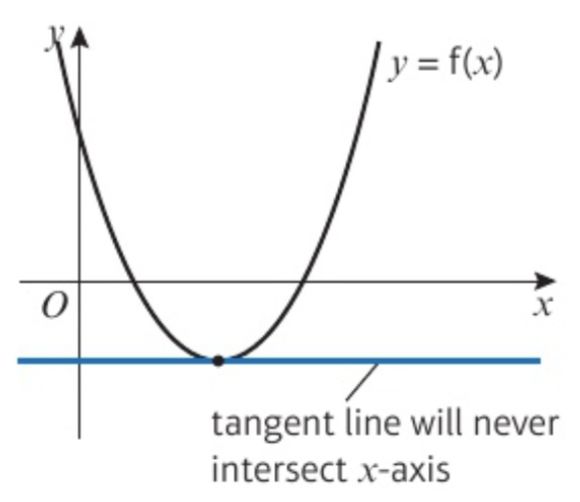
但這個方法也可能得不到近似解。當(dāng)選取的x0的值在turning point 時，公式中的分母等于0，方法就失效了。如圖所示：

這些細(xì)節(jié)在考試中都可能會考得到。下面我們通過三個例題來具體說明這一塊兒知識點的考法。

Part 2例題講解

1

分析：

(a)問考查一個知識點：

我們只需計算f(1）和f(2)的值即可證明。

(b)問考查用計算器帶入遞推公式求值。

(c)問考查畫圖。

解答：

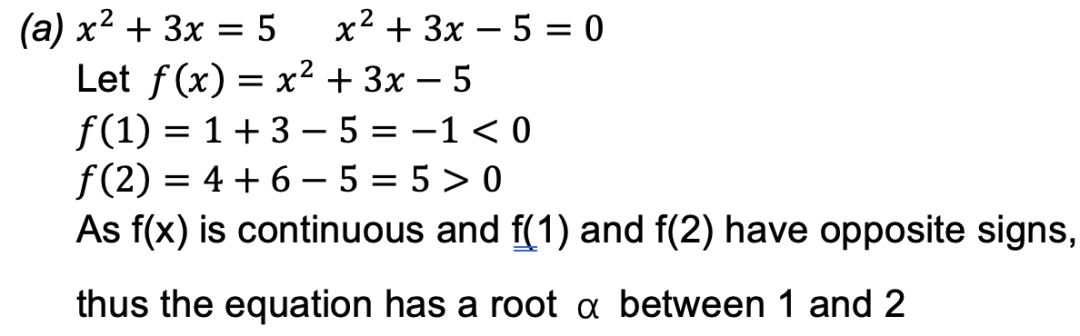
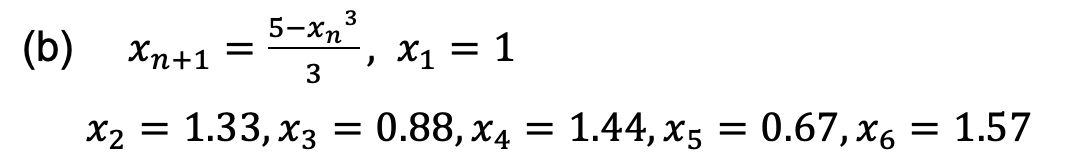
(c)

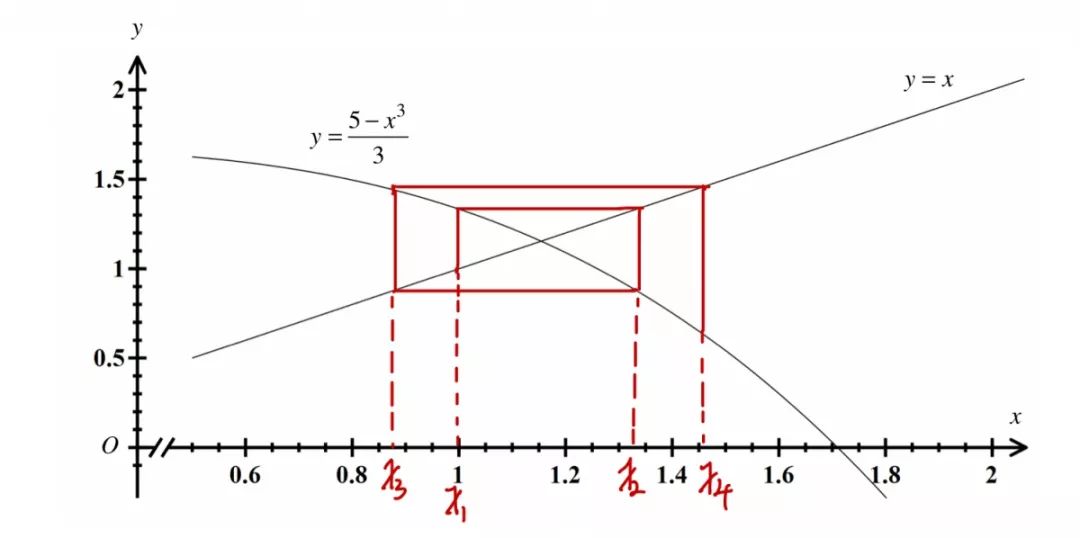
This iteration will diverge away from the root.

2

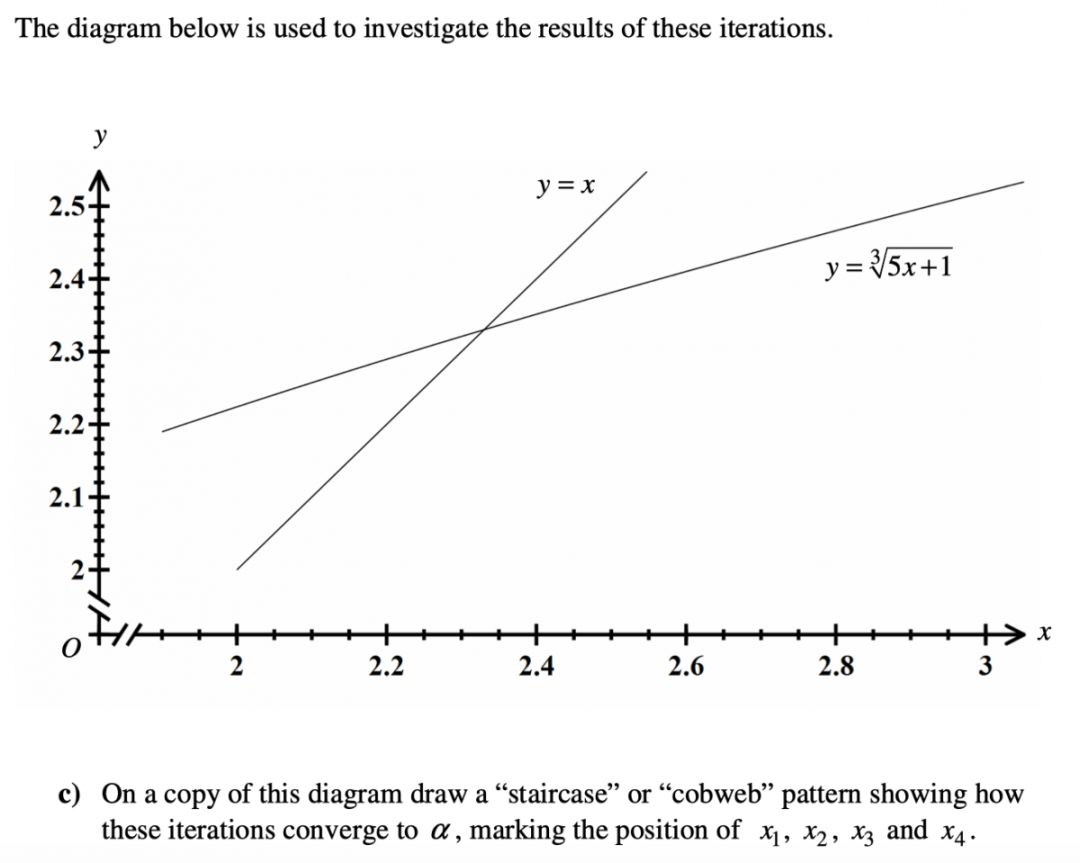
(a) (b)兩問同上面例題做法相同，留給同學(xué)們自己做。

(c)問的畫法如下圖所示：

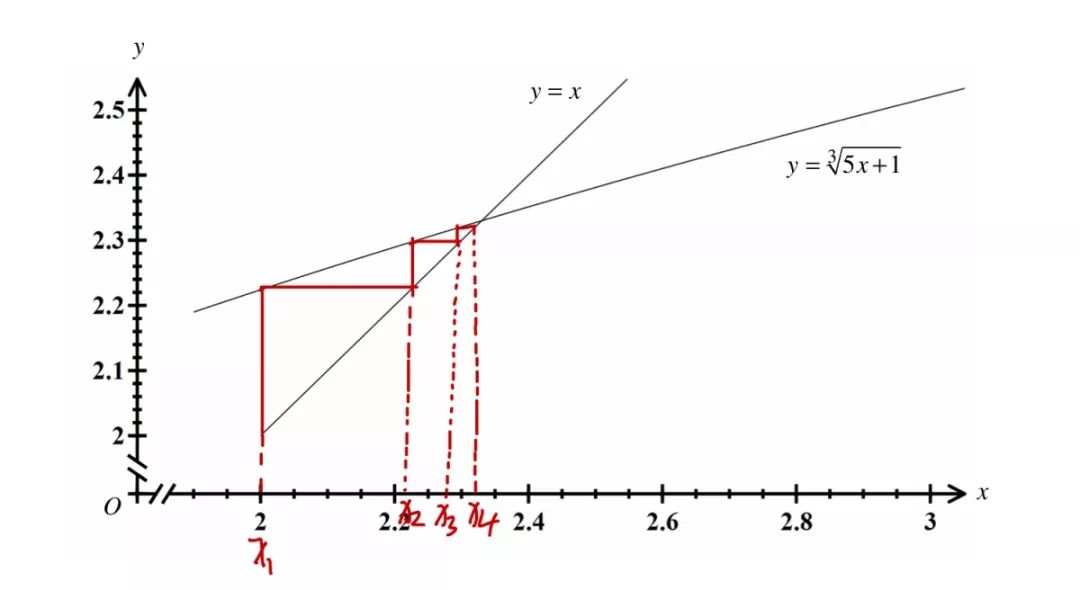
3

分析：

(a)問解釋在turning point處的x值為何不能作為遞推公式的起始值。(b)問考查遞推公式的計算。(c)問還是考查區(qū)間兩端的函數(shù)值變號時，在區(qū)間內(nèi)有根。但這個題需要我們選擇合適的區(qū)間。比如：

解答：