- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
IB DP Chemistry: HL復習筆記16.1.4 Rate Determining Step
Molecularity & Rate Determining Step
Rate-determining step & intermediates
- A chemical reaction can only go as fast as the slowest part of the reaction
- So, the?rate-determining step?is the slowest step in the reaction
- If a reactant appears in the rate-determining step, then the concentration of that reactant will also appear in the?rate equation
- For example, the rate equation for the reaction below is rate =?k[CH3Br][OH-]
CH3Br + OH-?→ CH3OH + Br-
-
- This suggests that both CH3Br and OH-?take part in the slow rate-determining step
- Molecularity?is the number of reactant particles that participate in the rate-determining step
- This reaction is a?bimolecular reaction
- Unimolecular: one species involved in the rate-determining step
- Bimolecular: two species involved in the rate-determining step
- The intermediate is derived from substances that react together to form it in the rate-determining step
- For example, for the reaction above the intermediate would consist of CH3Br and OH-

The intermediate formed from the species that are involved in the rate-determining step (and thus appear in the rate equation)
Exam Tip
Intermediates do not feature in rate equationsInstead, the chemicals required to make the intermediate feature in the rate equation
Identifying the rate-determining step
- The rate-determining step can be identified from a rate equation given that the reaction mechanism is known
- For example, propane (CH3CH2CH3) undergoes bromination under alkaline solutions
- The overall reaction is:
CH3CH2CH3?+ Br2?+ OH-?→ CH3CH2CH2Br + H2O + Br-
- The reaction mechanism is:

Reaction mechanism for the bromination of propane under alkaline conditions
- The rate equation is:
Rate =?k[CH3CH2CH3][OH-]
- From the rate equation, it can be deduced that only CH3CH2CH3?and OH-?are involved in the rate-determining step and not bromine (Br2)
- CH3CH2CH3?and OH-?are only involved in the first step of the reaction mechanism, therefore the rate-determining step is:
- CH3CH2CH3?+ OH-?→?CH3CH2CH2-?+ H2O
Potential Energy Level Profiles
Single-step reactions
- When any reacting molecules collide with bond breaking and bond formation occurring, the interacting molecules will be in an unstable, high-energy state temporarily
- This?transition state?will be of a higher energy than either the reactants or products and corresponds to the activation energy
- The exothermic reaction of hydrogen and iodine to form hydrogen iodide will be used to discuss how energy level diagrams relate to the rate-determining step
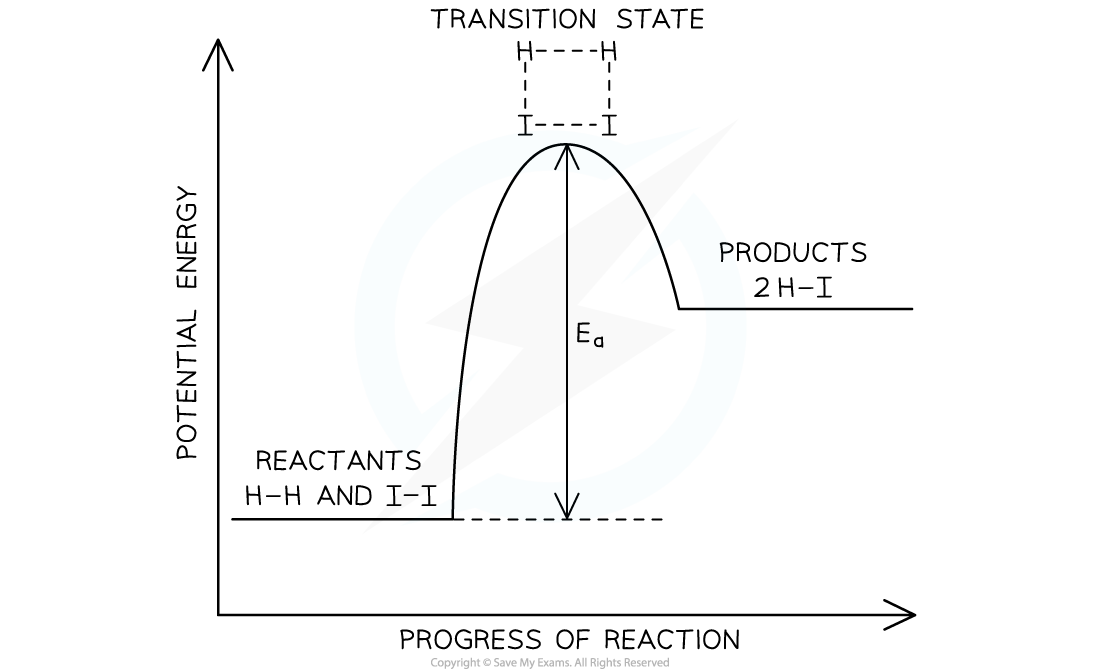
The potential energy level diagram for the exothermic reaction of hydrogen and iodine
- As the reaction proceeds, covalent bonds start to form between the hydrogen and iodine atoms from the hydrogen and iodine molecules
- At the same time, the covalent bonds within the hydrogen and iodine molecules grow longer and become weaker
- This results in the transition state complex shown

The transition state complex for the reaction of hydrogen and iodine
- From this transition state, the bonds between the hydrogen and iodine atoms can continue to grow shorter and stronger resulting in the formation of hydrogen iodide
- Alternatively, the bonds within the hydrogen and iodine molecules can grow shorter and stronger which would result in the formation of the reactants
- Hydrogen iodide will?only?form if the hydrogen and iodine molecules collide with kinetic energy greater than or equal to the activation energy
- The molecules will also need to collide in the correct orientations
- The reaction, or elementary, step with the greatest activation energy will be the rate-determining step and can be used to determine the rate equation
Multi-step reactions
- The endothermic reaction of nitrogen dioxide and fluorine to form nitryl fluoride (NO2F) will be used to relate rate equations and rate-determining steps to the energy level diagram of a multi-step reaction:
2NO2?(g) + F2?(g) → 2NO2F (g)
- This reaction is unlikely to occur in a single step as that would require three molecules to collide in the correct orientation and with sufficient kinetic energy
- This is even less likely to occur as all three molecules are gaseous
- Experimental data shows that the rate equation for this reaction is:
Rate =?k[NO2][F2]
- One proposed reaction mechanism for this reaction involves the following elementary steps:
- Step 1: NO2?+ F2?→ NO2F + F
- Step 2: NO2?+ F → NO2F
- Step 1?must be the rate-determining step as it is the only step that has reactants matching the rate equation
- Therefore, on a potential energy level diagram the activation energy for step 1 will be greater than the activation energy for step 2
- The transition state for this multi-step reaction must be:
NO2?+ NO2F + F
-
- This can be deduced using the the equation for elementary step 1 and the overall equation
- The overall equation states that two NO2?react with one F2
- Elementary step 1 uses one?NO2?to form NO2F + F
- This leaves one?NO2?along with NO2F + F
- This can be deduced using the the equation for elementary step 1 and the overall equation
- This leads to the following potential energy level diagram:
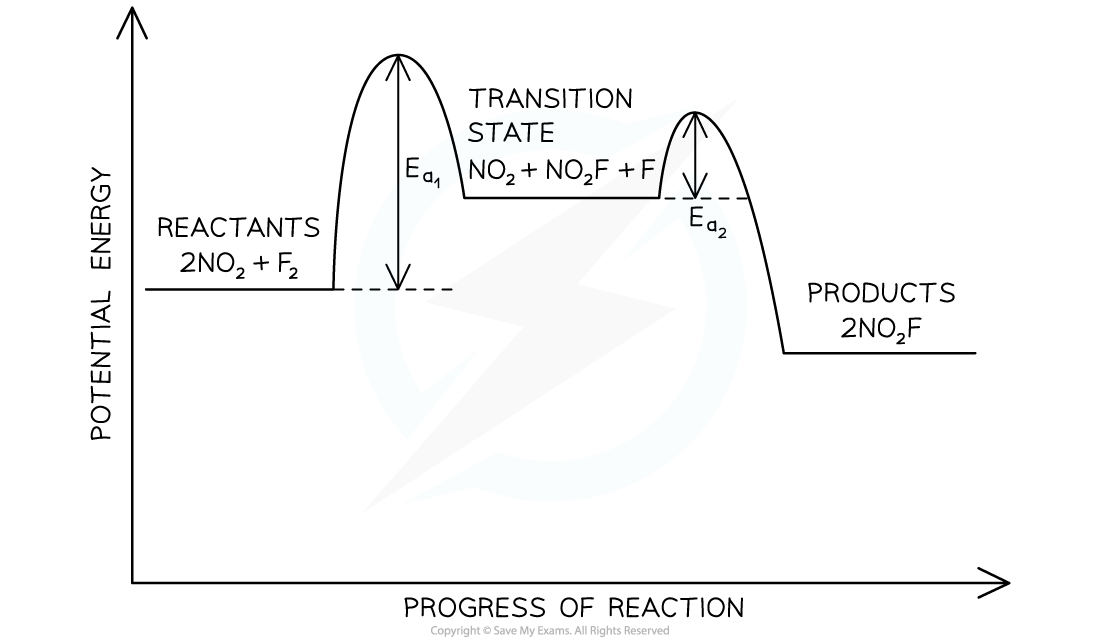
Potential energy level diagram for the formation of nitryl fluoride
- Key points from the potential energy level diagram are:
- The overall reaction is endothermic, as stated
- The rate-determining step is the step that has the greatest activation energy
- There is a labelled energy level for the transition state
Exam Tip
Multi-step reactions where the first elementary step is not the rate-determining step prove more challenging in terms of potential energy level diagrams. Remember that the rate-determining step?must?have the greatest activation energy. Do not confuse greatest with the highest! When people talk about the highest they are normally referring to where the activation energy peak is, not the actual value it represents
Catalysts & Mechanisms
Identifying intermediates & catalyst
- When a rate equation includes a species that is not part of the chemical reaction equation then this species is a [popover id="mT5UZwSwYE9Vt6Fl" label=catalyst]
- For example, the halogenation of butanone under acidic conditions
- The overall equation for this reaction is:

- One commonly accepted reaction mechanism is:
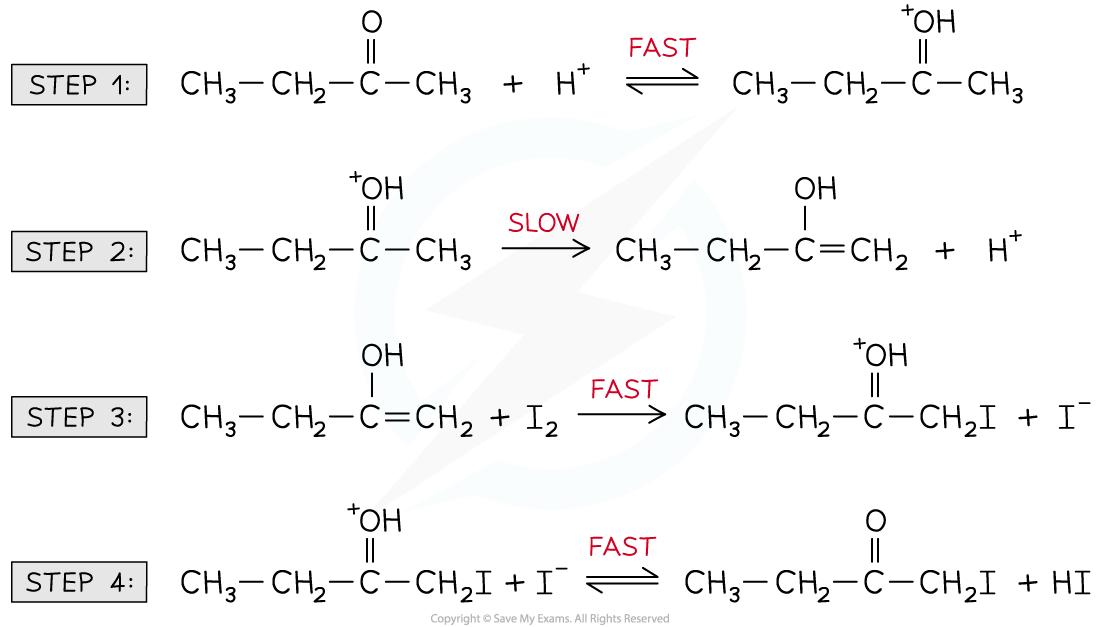
Reaction mechanism for the halogenation of butanone under acidic conditions
- The rate-determining step is the slowest step, identified as step 2
- However, the CH3CH2C(OH+)CH3?cannot be used in the rate equation as it is an intermediate, not a reactant

Reaction to form the intermediate found in the rate-determining step
- Therefore, the CH3CH2COCH3?and H+?that form the intermediate feature in the rate equation:
Rate =?k[CH3CH2COCH3][H+]
- The H+?is?not?a reactant in the overall chemical equation but it does appear in the rate equation
- H+?must, therefore, be a?catalyst
- This is also supported by the?H+?being used in step 1 and forming as a product in step 2
轉載自savemyexams

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









