- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
IB DP Physics: HL復習筆記10.2.6 Orbital Motion, Speed & Energy
Orbital Motion, Speed & Energy
- Since most planets and satellites have a near circular orbit, the gravitational force?FG?between the sun or another planet provides the?centripetal force?needed to stay in an orbit
- Both the gravitational force and centripetal force are?perpendicular?to the direction of travel of the planet
- Consider a satellite with mass?m?orbiting Earth with mass?M?at a distance?r?from the centre travelling with linear speed?v
FG?=?Fcirc
- Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:

- Where:
- v?= linear speed of the mass in orbit (m s-1)
- G?=?Newton's Gravitational Constant
- M?= mass of the object being orbited (kg)
- r?= orbital radius (m)
- This means that all satellites,?whatever their mass, will travel at the same speed?v?in a particular orbit radius?r
- Since the direction of a planet orbiting in circular motion is constantly changing, the?centripetal acceleration acts towards the planet
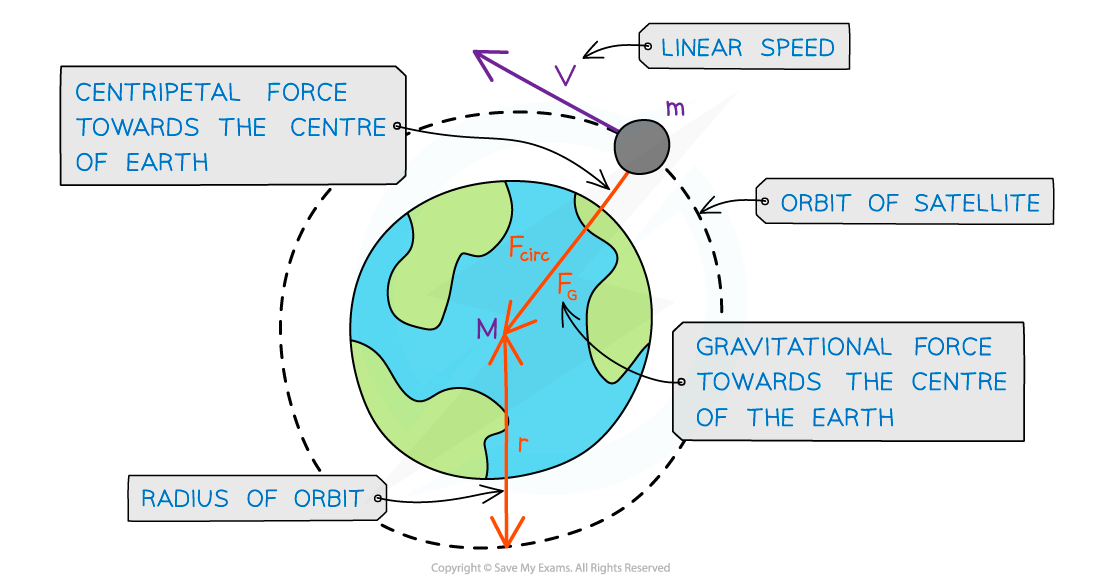
- Since the direction of a planet orbiting in circular motion is constantly changing, the?centripetal acceleration acts towards the planet
A satellite in orbit around the Earth travels in circular motion
Time Period & Orbital Radius Relation
- Since a planet or a satellite is travelling in circular motion when in order, its orbital time period?T?to travel the circumference of the orbit 2πr, the linear speed?v is:
 Graphical Representation of T2?∝ r3
Graphical Representation of T2?∝ r3
- The relationship between?T?and?r?can be shown using a logarithmic plot
- T2?∝ r3
- 2 × log(T)?∝ 3 × log(r)
- The graph of log(T) in years against log(r) in AU (astronomical units) for the planets in our solar system is a straight line graph:
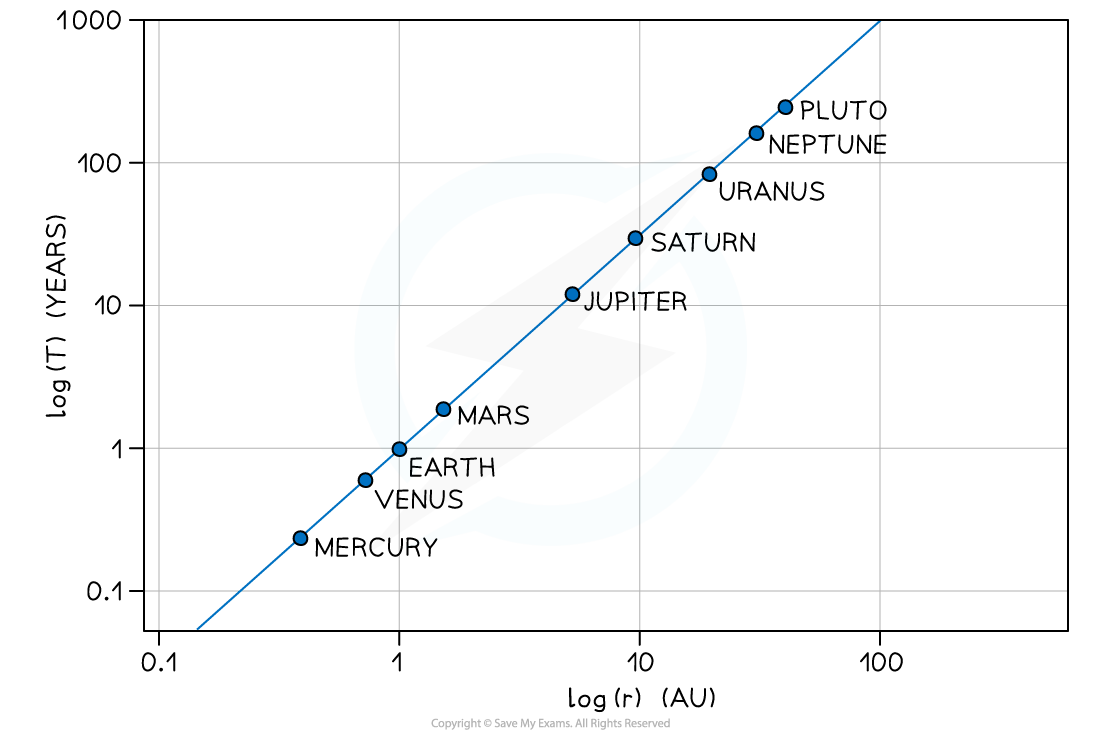
- The graph does not go through the origin since it has a negative y-intercept
- Only the log of both?T?and?r?will produce a straight line graph
Worked Example
A binary star system constant of two stars orbiting about a fixed point?B. The star of mass?M1?has a circular orbit of radius?R1?and mass?M2?has a radius of?R2. Both have linear speed?v?and an angular speed ? about?B.
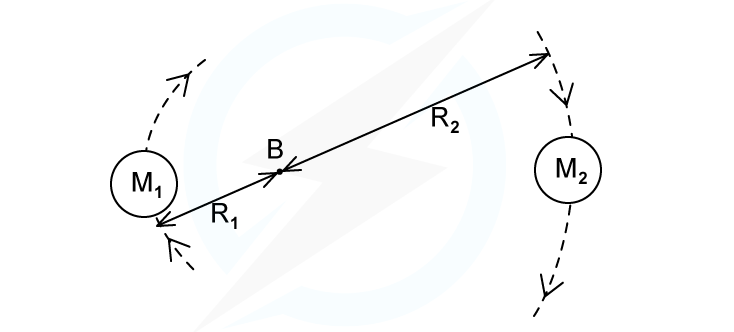
State the following formula, in terms of?G,?M2,?R1?and?R2
(i) The angular speed ? of?M1
(ii) The time period?T?for each star in terms of angular speed ?


Energy of an Orbiting Satellite
- An orbiting satellite follows a circular path around a planet
- Just like an object moving in circular motion, it has both kinetic energy (KE)?and?gravitational potential energy (GPE) and its?total?energy is always?constant
- An orbiting satellite's total energy is calculated by:
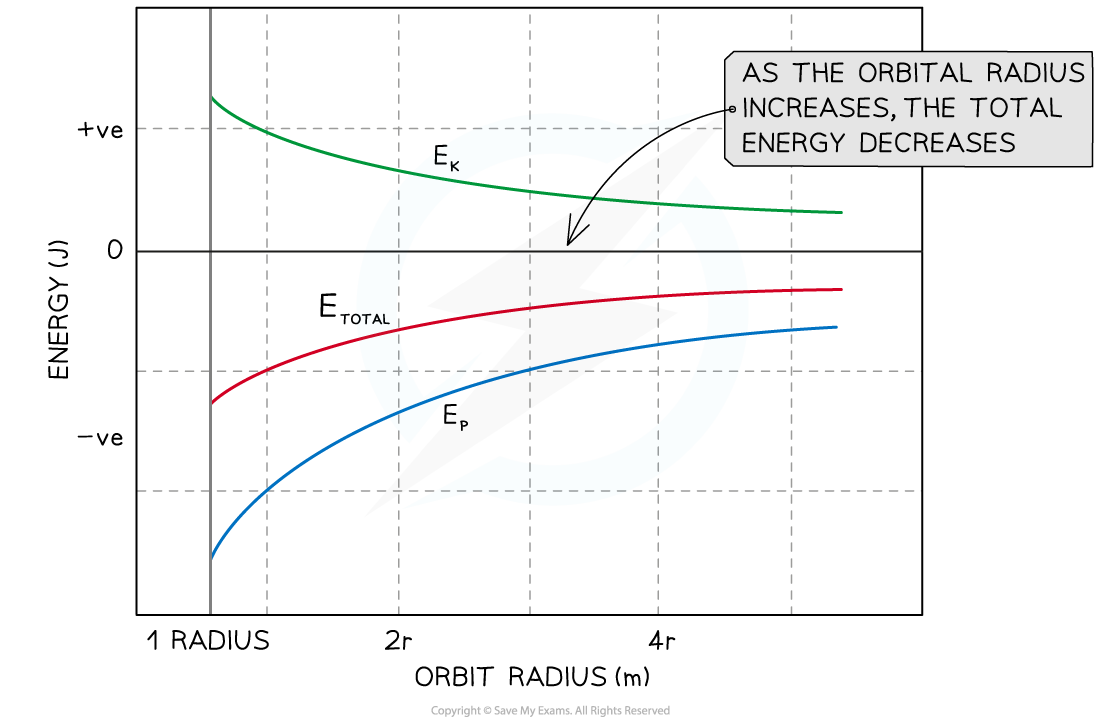
A graph showing the kinetic, potential and total energy for a mass at varying orbital distances from a massive body
Total energy = Kinetic energy + Gravitational potential energy
- This means that the satellite's KE and GPE are also both constant in a particular orbit
- If the orbital radius of a satellite?decreases?its KE?increases?and its GPE?decreases
- If the orbital radius of a satellite?increases?its KE?decreases?and its GPE?increases
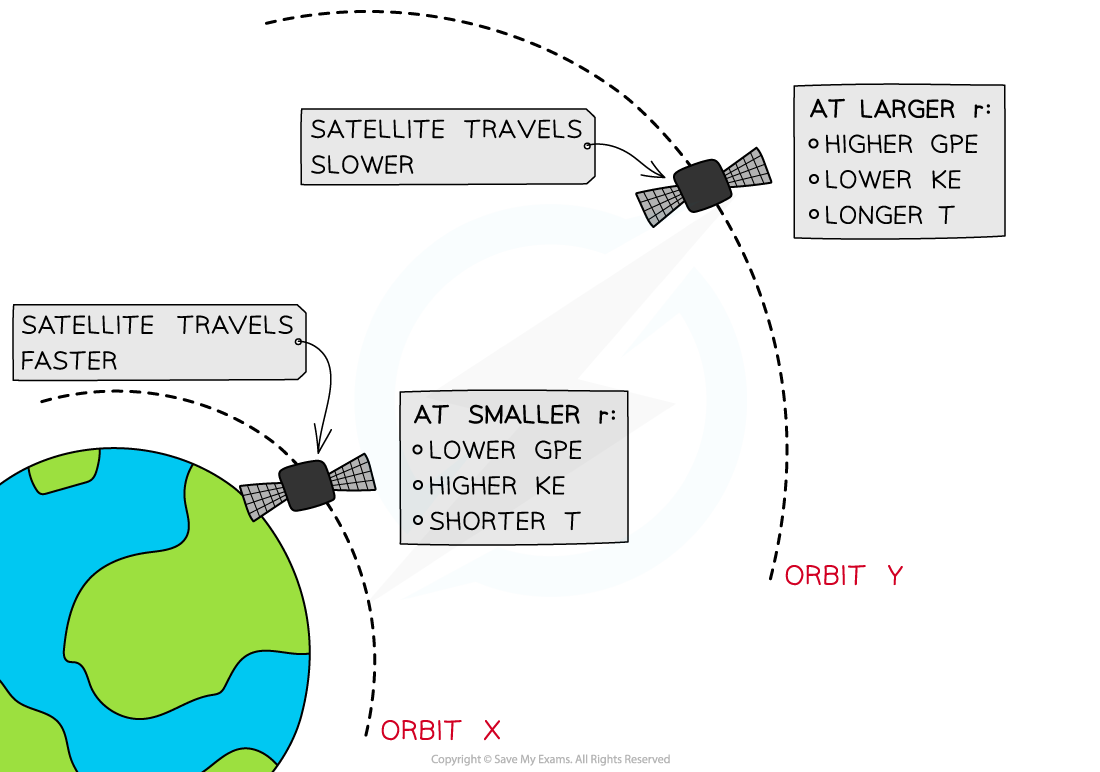
At orbit Y, the satellite has greater GPE and less KE than at at orbit X
- A satellite is placed in two orbits,?X and Y, around Earth
- At orbit X, where the radius of orbit?r?is smaller, the satellite has a:
- Larger gravitational force on it
- Higher speed
- Higher KE
- Lower GPE
- Shorter orbital?time period,?T
- At orbit Y, where the radius of orbit?r?is larger, the satellite has a:
- Smaller gravitational force on it
- Smaller speed
- Lower KE
- Higher GPE
- Longer orbital time period,?T
Worked Example
Two satellites A and B, of equal mass, orbit a planet at radii?R?and?3R?respectively. Which one of the following statements is incorrect?
A? ?A has more kinetic energy and less potential energy than B
B? ?A has a shorter time period and travels faster than?B
C? ?B has less kinetic energy and more potential energy than A
D? ?B has a longer time period and travels faster than A
ANSWER:? ? D
-
- Since B is at a larger orbital radius (3R?instead of?R) it has a longer time period since?T2?∝ R3?for an orbiting satellite
- However, satellite B will travel much slower than A
- Its larger orbital radius means the force of gravity will be much lower for B than for A
Exam Tip
Orbital Energy Calculations
- A synchronous orbit is:
When an orbiting body has a time period equal to that of the body being orbited and in the same direction of rotation as that body
- These usually refer to?satellites?(the orbiting body) around?planets?(the body being orbited)
- The orbit of a synchronous satellite can be above any point on the planet's surface and in any plane
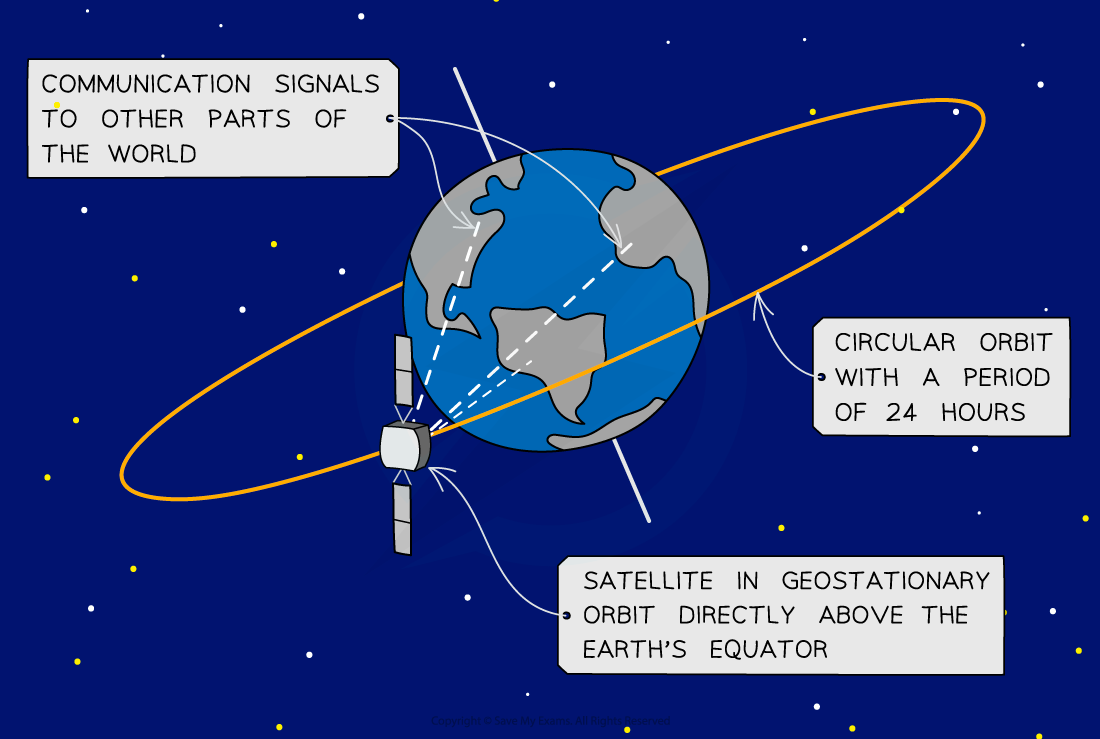
- When the plane of the orbit is directly above the equator, it is known as a?geosynchronous?orbit
Geostationary Orbit
- Many communication satellites around Earth follow a?geostationary orbit
- This is sometimes referred to as a?geosynchronous?orbit
- This is a specific type of orbit in which the satellite:
- Remains directly?above the equator
- Is in the?plane of the equator
- Always orbits at the?same point?above the Earth’s surface
- Moves from?west to east?(same direction as the Earth spins)
- Has an orbital time period equal to Earth’s rotational period of?24 hours
- Geostationary satellites are used for?telecommunication?transmissions (e.g. radio) and television broadcast
- A base station on Earth sends the TV signal up to the satellite where it is amplified and broadcast back to the ground to the desired locations
- The satellite receiver dishes on the surface must point towards the same point in the sky
- Since the geostationary orbits of the satellites are fixed, the receiver dishes can be fixed too
Low Orbits
- Some satellites are in low orbits, which means their altitude is closer to the Earth's surface
- One example of this is a?polar?orbit, where the satellite orbits around the north and south pole of the Earth
- Low orbits are useful for taking high-quality photographs of the Earth's surface. This could be used for:
- Weather
- Military applications
Geostationary satellite in orbit
Worked Example
Orbital Motion
- When a satellite is moving in orbital motion, the velocity of the satellite will be given by:

- Where
- ET?= The total energy of the satellite (J)
- EP?= The potential energy of the satellite (J)
- EK?= The kinetic energy of the satellite (J)
- v?= the velocity of the satellite (m s-1)
- M = mass of the Earth (or large body being orbited) (kg)
- m = mass of satellite or orbiting object (kg)
- G?= ?The gravitational constant?=?6.67 x 10-11?Nm2kg-2
- r?= the orbital radius of the satellite (m)
轉載自savemyexams

最新發(fā)布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1










