• There is a universal force of attraction between all matter with?mass
  • This force is known as the ‘force due to gravity’ or the?weight

• The Earth’s gravitational field is responsible for the weight of all objects on Earth
• A gravitational field is defined as:

A region of space where a test mass experiences a force due to the gravitational attraction of another mass

• The direction of the gravitational field is always towards the centre of the mass causing the field
  • Gravitational forces?cannot?be repulsive
• Gravity has an infinite range, meaning it affects all objects in the universe
  • There is a?greater?gravitational force around objects with a?large mass?(such as planets)
  • There is a?smaller?gravitational force around objects with a?small mass?(almost negligible for atoms)

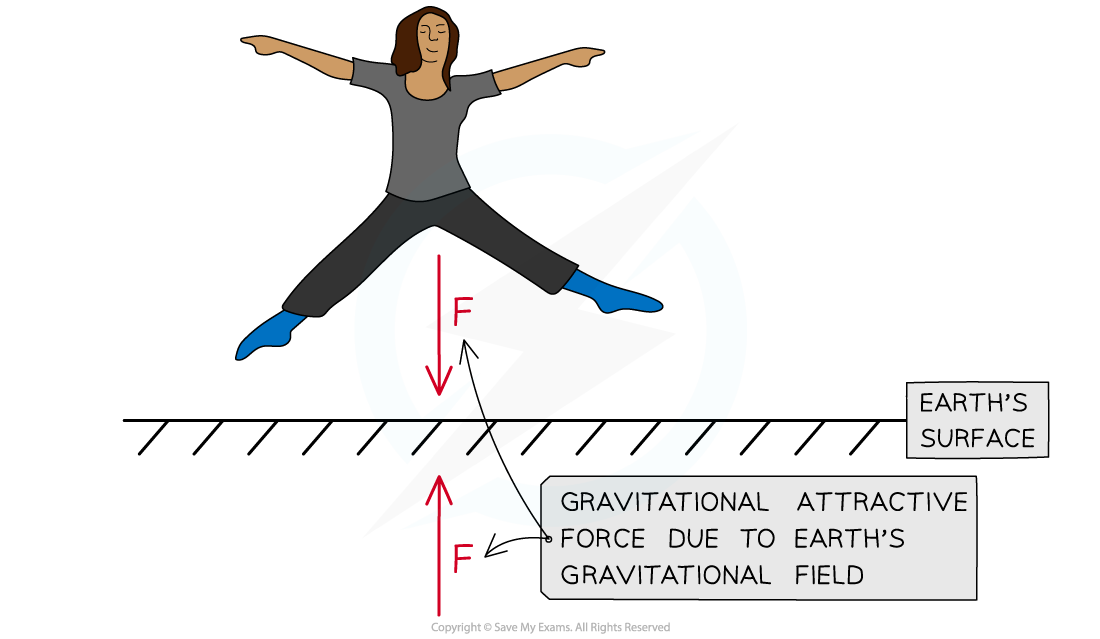
The Earth's gravitational field produces an attractive force. The force of gravity is always attractive

• The gravitational field strength at a point is defined as:

The force per unit mass experienced by a test mass at that point

• This can be written in equation form as:

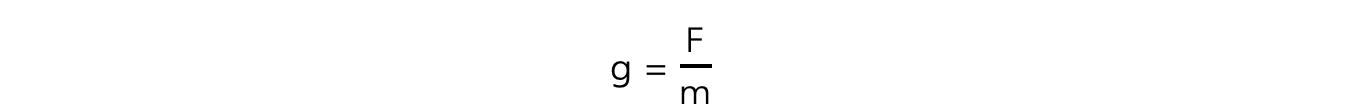
• Where:
  • g?=?gravitational field strength?(N kg?1)
  • F?= force due to gravity, or weight (N)
  • m?= mass of test mass in the field (kg)

• This equation shows that:
  • On planets with a large value of?g, the gravitational force per unit mass is?greater?than on planets with a smaller value of?g

• An object's mass remains the?same?at all points in space
  • However, on planets such as Jupiter, the?weight?of an object will be greater than on a less massive planet, such as Earth
  • This means the gravitational force would be so high that humans, for example, would not be unable to fully stand up

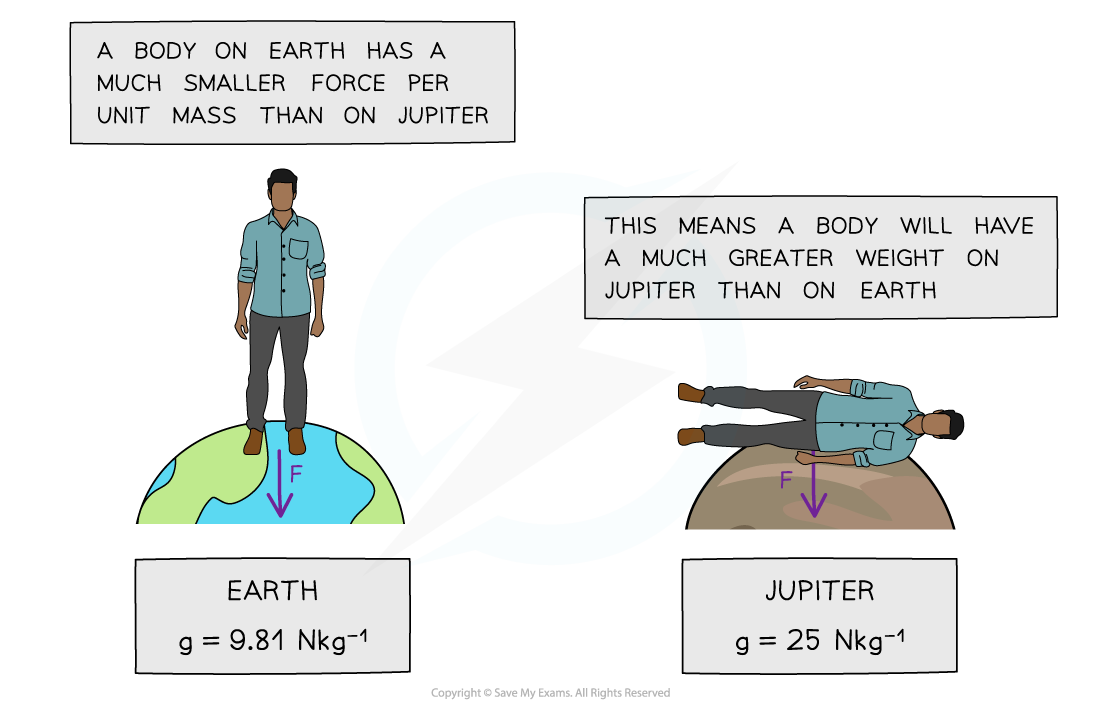
A person’s weight on Jupiter would be so large that a human would be unable to fully stand up

• Factors that affect the gravitational field strength at the surface of a planet are:
  • The?radius?r?(or diameter) of the planet
  • The?mass?M?(or density) of the planet

• This can be shown by equating the equation?F?=?mg?with Newton's law of gravitation:

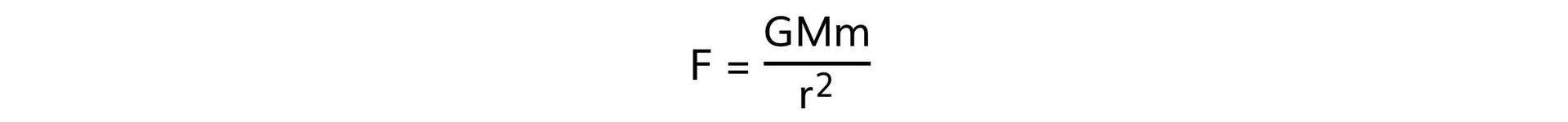
• Substituting the force?F?with the gravitational force?mg?leads to:

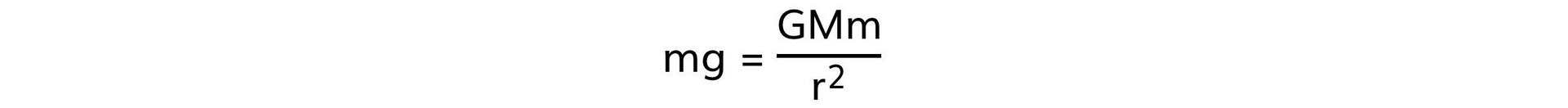
• Cancelling the mass of the test mass,?m, leads to the equation:

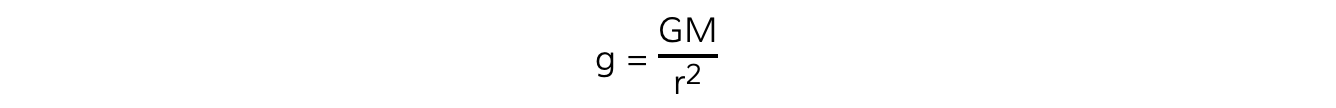
• Where:
  • G?=?Newton's Gravitational Constant
  • M = mass of the body causing the field (kg)
  • r?= distance from the mass where you are calculating the field strength (m)
• This equation shows that:
  • The gravitational field strength?g?depends only on the mass of the body?M?causing the field
  • Hence, objects with any mass?m?in that field will experience the?same gravitational field strength
  • The gravitational field strength?g?is?inversely proportional?to the?square?of the radial distance,?r2

• In a similar way to other vectors, such as force or velocity, the gravitational field strength due to two bodies can be determined
  • This is because gravitational field strength is a vector, meaning it has both a magnitude and direction

• The resultant gravitational field strength is, therefore, the vector sum of the gravitational field strength due to each body

Step 1: List the known quantities

• • Mass of one star,?M?= 5.0 × 10³⁰?kg
  • Distance between one star and the planet,?r?= 3.0 × 10¹²?m
  • Angle between the gravitational field strength and the planet, θ = 42°

Step 2: Write out the equation for gravitational field strength

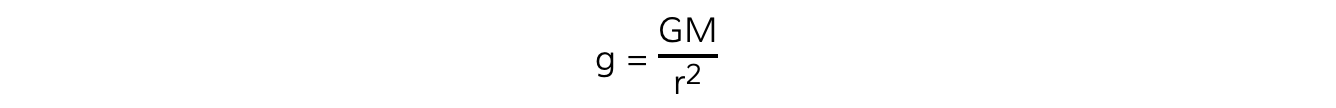Step 3: Calculate the gravitational field strength due to one star

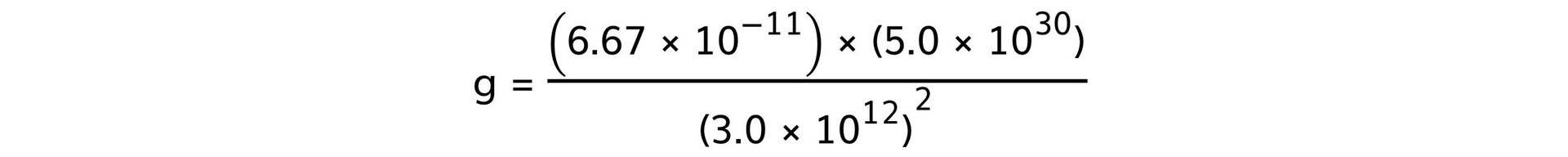g?= 3.7 × 10^?5N kg^?1

Step 4: Resolve the vectors vertically

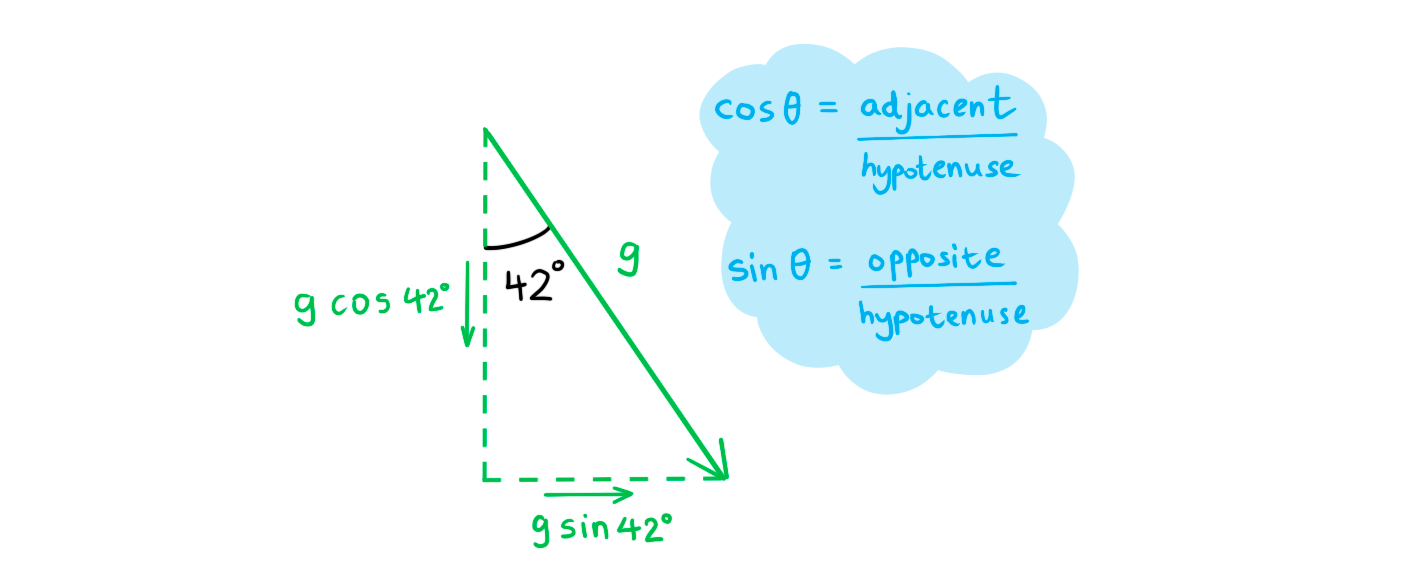
• • The vertical component of each vector is?g?cos 42°

Step 5: Use vector addition to determine the resultant gravitational field strength

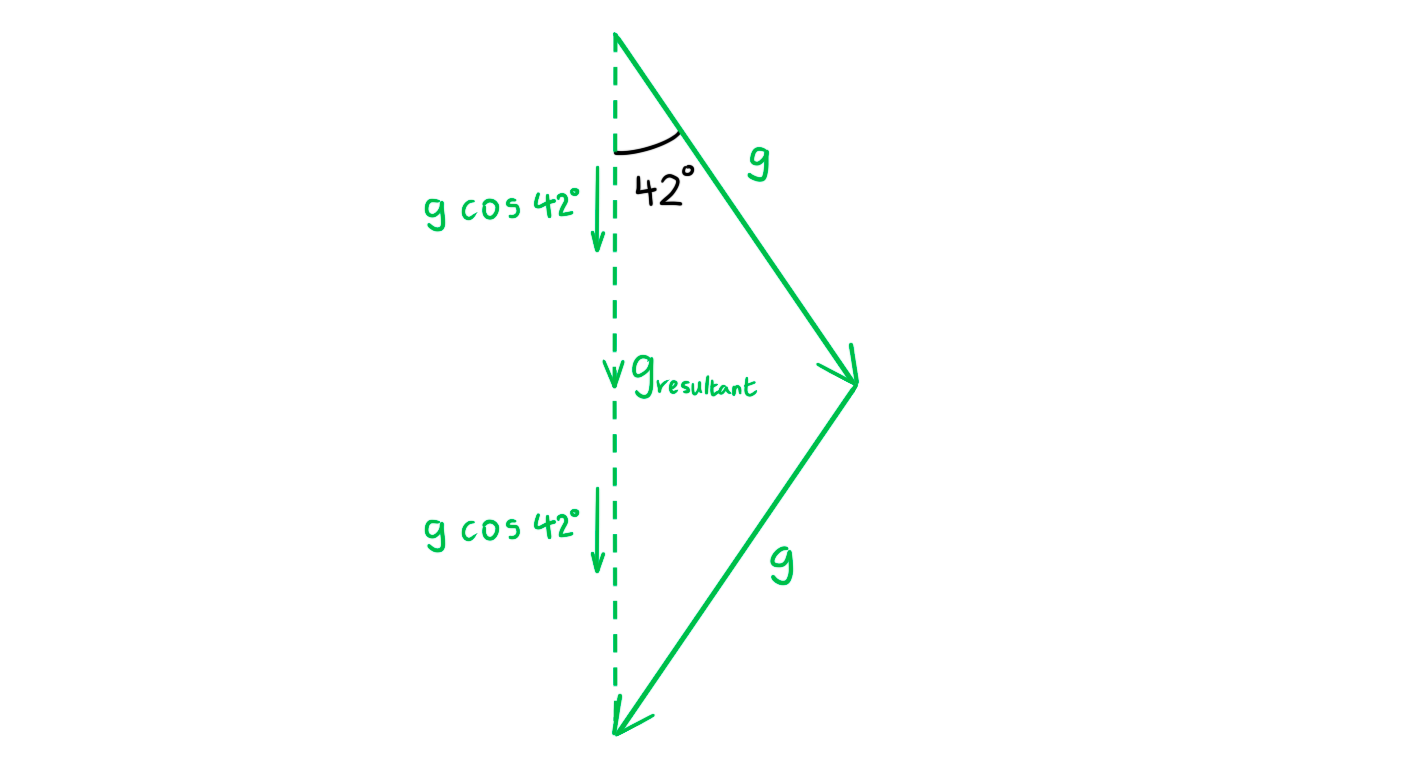gresultant?=?g?cos 42° +?g?cos 42° = 2g?cos 42°

gresultant?= 2 × (3.7 × 10^?5) × cos 42°

gresultant?= 5.5 × 10^?5?N kg^?1