Aim of the Experiment

• The aim of the experiment is to investigate the half-life of a decaying radioactive sample
  • This can be done with a live sample if safe access is available
  • This can also be done through an online simulation

Variables

• Independent variable?= time,?t
• Dependent variable?= radioactive activity,?A
• Control variables:
  • Size of sample
  • Same distance from detector to sample
  • Same material for sample

Equipment List

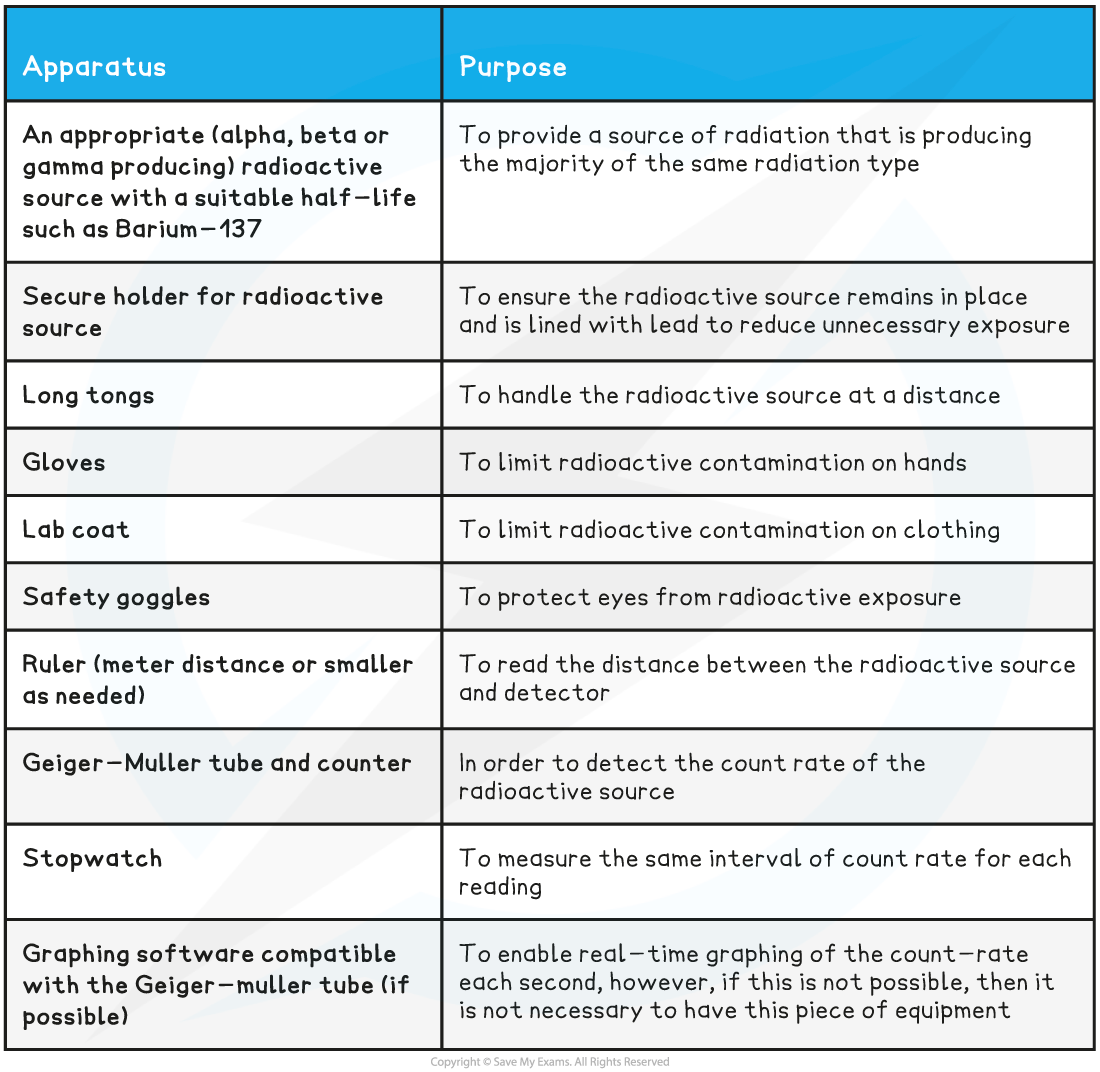
• Resolution?of equipment:
  • Metre ruler = 1 mm
  • Stopwatch = 0.01 s

Method

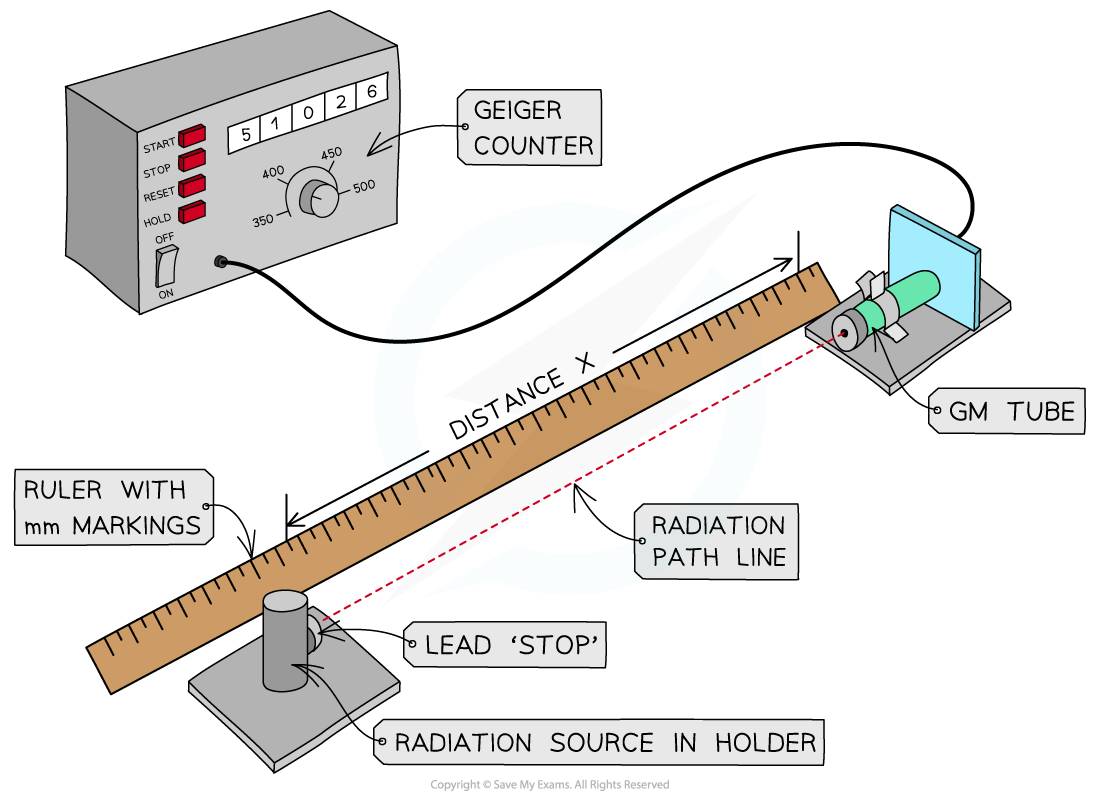
1. Measure the background radiation for 30 second intervals using a Geiger-Muller tube without the radiation source in the room, take several readings and find an average
2. Next, put the radiation source at a set starting distance appropriate for the ionizing strength of the radiation (e.g. 1 - 2 cm for an alpha source, 2 - 5 cm for a beta source and 15 - 30 cm for a gamma source) from the GM tube
3. If graphing software is available to use with the Geiger-Muller tube, then that should be started as soon as the source is placed in position, if not, then proceed to step 4
4. Once the sample is in place measure the number of counts in 30-second intervals for 10 minutes or until the activity greatly decreases from the beginning value
5. Remove sample and replace into a lead-lined box or safe storage container
6. Repeat this for several trials if possible using fresh same size samples

A suitable table of results might look like this:

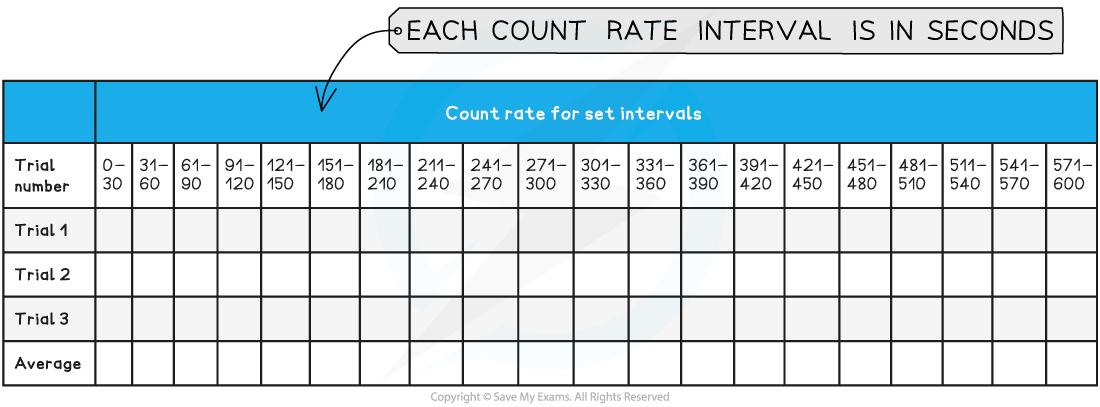
Analysis of Results

• What is important for this experiment is the initial count rate and the following decrease as the radioactive source decays from the?parent nuclei?into the?daughter nuclei.
  • The background rate?must be subtracted?from the data before analysis can begin. This is true for both graphed and manual data

• In order to see the decrease and model it, the data should be graphed with the correct count rate (background subtracted) on the y-axis and the time intervals on the x-axis. If graphing software is used then the graph should look similar to the following:

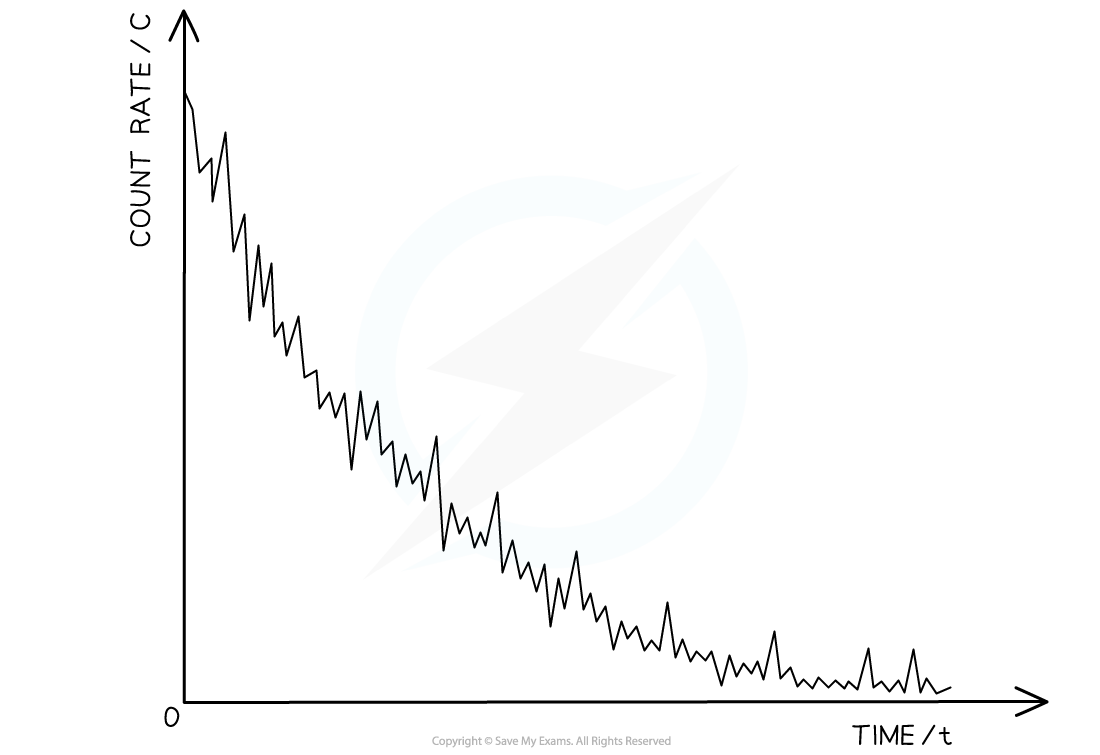
• However, if the manual method is used, then there will be twenty data points rather than a smooth curve with fluctuations
• Using this curve, the half-life can be found by comparing the initial magnitude of the activity with the time it takes to decay to half of the original activity.
  • This can be extended by finding the time taken for two half-lives to pass and the activity to reach one quarter for quantitative comparison

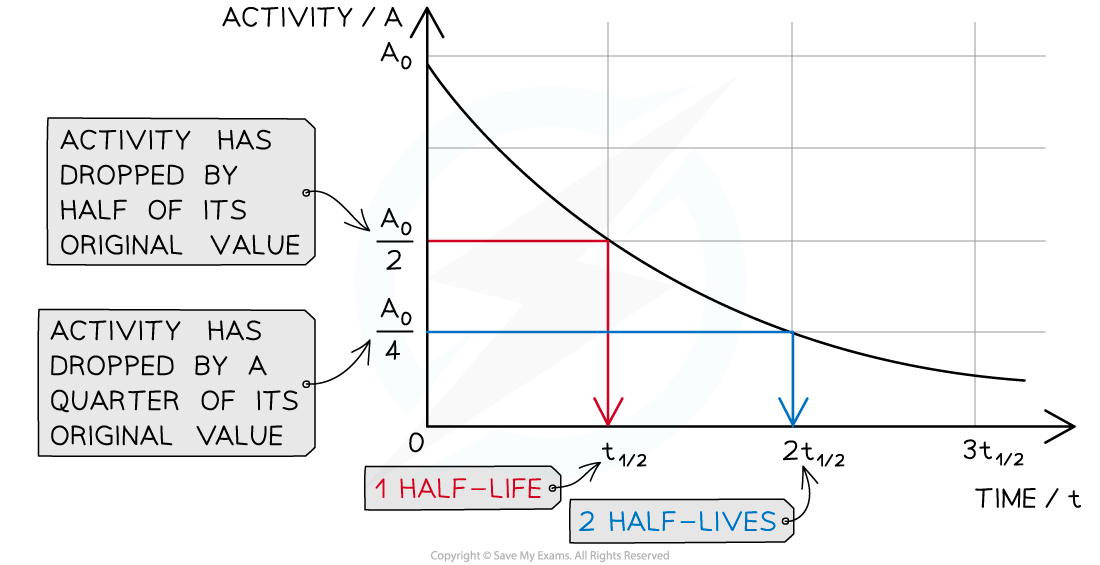
• Compare found half-life for the radioactive sample with the known value

Evaluation

Systematic errors:

• The Geiger counter may suffer from an issue called “dead time”
  • This is when multiple counts happen simultaneously within ~100 μs and the counter only registers one
  • This is a more common problem in older detectors, so using a more modern Geiger counter should reduce this problem

• If this experiment is done manually, there will be uncertainty in the time
  • This uncertainty in time intervals will mean variation in counting intervals, however, due to the 30-second interval and the nature of this experiment this is not easily accounted for
  • It is best to discuss what these uncertainties could mean for the results of this experiment

Random?errors:

• Radioactive decay is?random, so repeat readings are vital in this experiment
• Measure the count over an appropriate time span such as 30 seconds
  • A larger count helps reduce the statistical percentage uncertainty inherent in smaller readings
  • This is because the percentage error is proportional to the inverse-square root of the count
  • However, a shorter count will mean that more data points are available to help make an appropriate decay curve

Safety Considerations

• For any radioactive source:
  • Reduce the exposure time by keeping it in a lead-lined box when not in use
  • Handle with long tongs
  • Avoid physical contact and handle the source with care
  • Do not point the source at anyone and keep a large distance (as activity reduces by an inverse square law)

• Safety clothing such as a lab coat, gloves and goggles must be worn

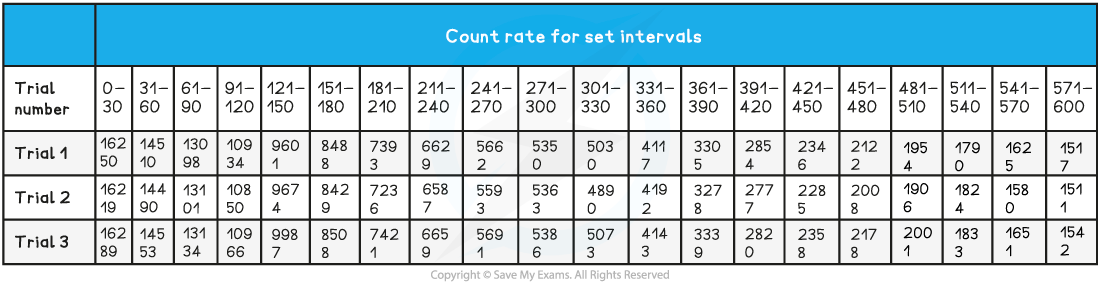
Step 1: Determine a mean value of background radiation

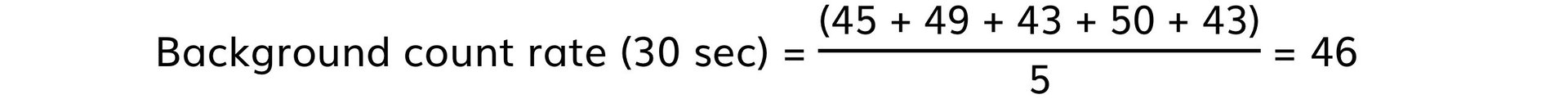
Step 2: Calculate C (corrected average count rate)

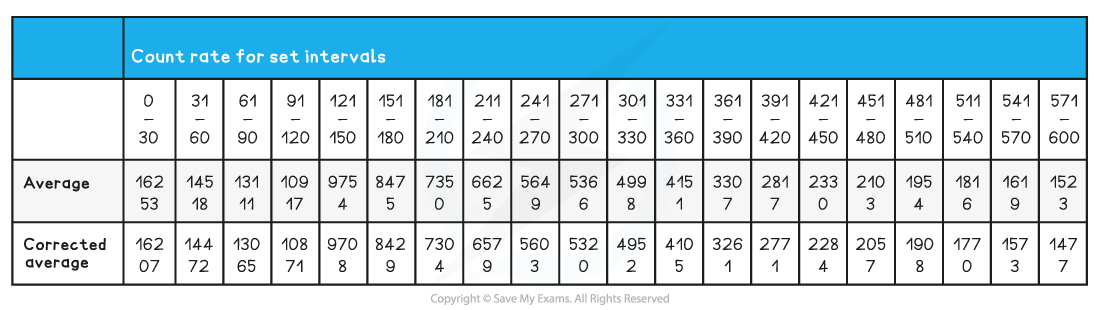
Step 3: Plot a graph of C against?t?(time in 30-sec intervals) and add a smooth-fitting curve

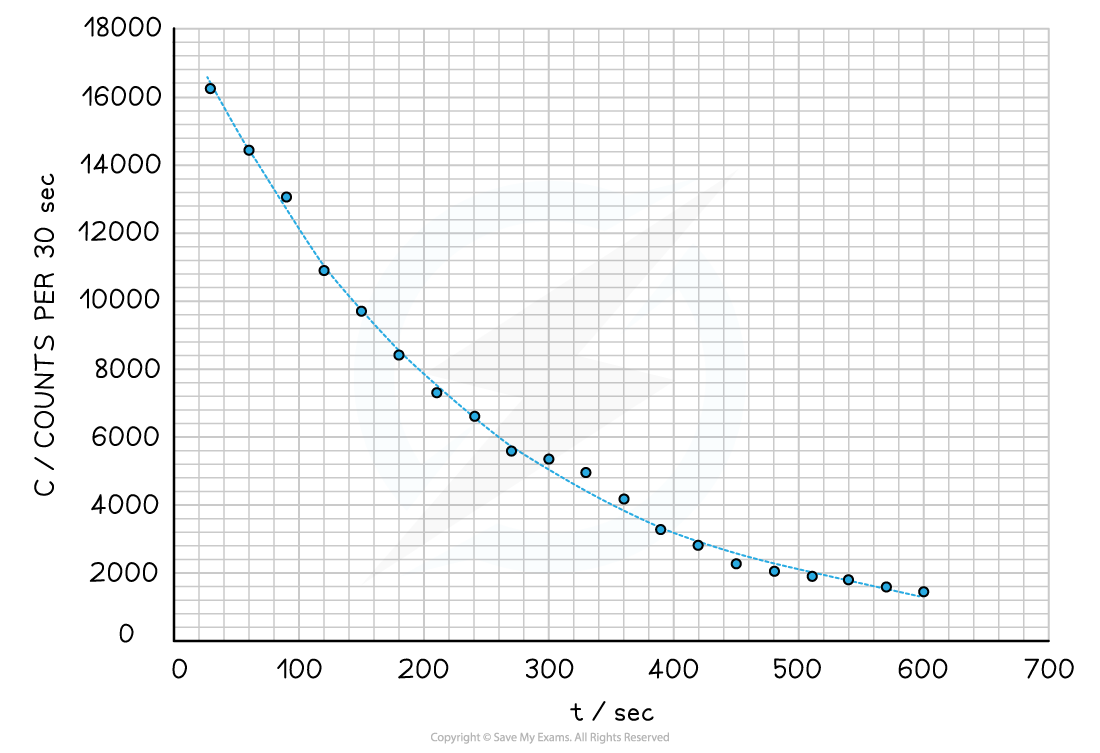
Step 4: Map the first three half-lives use the curve

• • The first half-life took approximately 160 seconds to occur
  • The second half-life took approximately 150 seconds to be reached following the first half-life
  • The third half-life took approximately 155 seconds to be reached following the second half-life

  

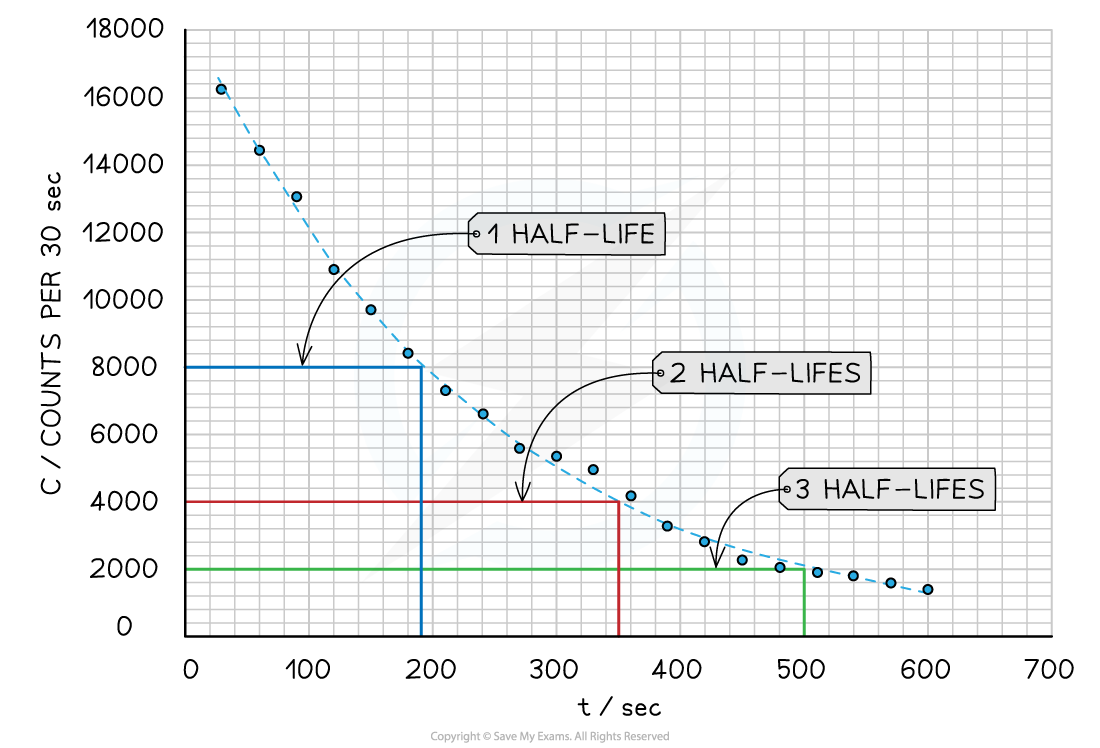
Step 5: Average the half-lives

(160 + 150 + 155) ÷ 3 = 155 seconds

Step 6: State the final answer

• • The final found answer was?155 seconds?for the half-life of this sample data