- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
CIE A Level Chemistry復習筆記5.6.1 Basics of Kinetics
Kinetics: Basics
- The?rate of reaction?refers to the change in the amount or concentration of a reactant or product per unit time and can be found by:
- Measuring the?decrease in the concentration of a reactant?OR
- Measuring the?increase in the concentration of a product?over?time
- The units of rate of reaction are mol dm-3?s-1
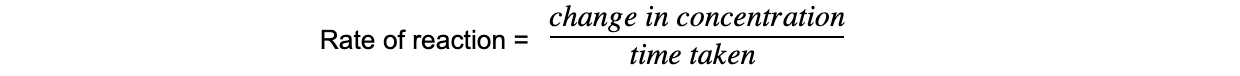
Rate equation
- The?thermal decomposition?of calcium carbonate (CaCO3) will be used as an example to study the rate of reaction
CaCO3?(s) → CaO (s) + CO2?(g)
- The rate of reaction at different concentrations of CaCO3?is measured and tabulated

Rate of reactions table

- A?directly proportional?relationship between the?rate?of the reaction and?concentration?of CaCO3?is observed when a graph is plotted
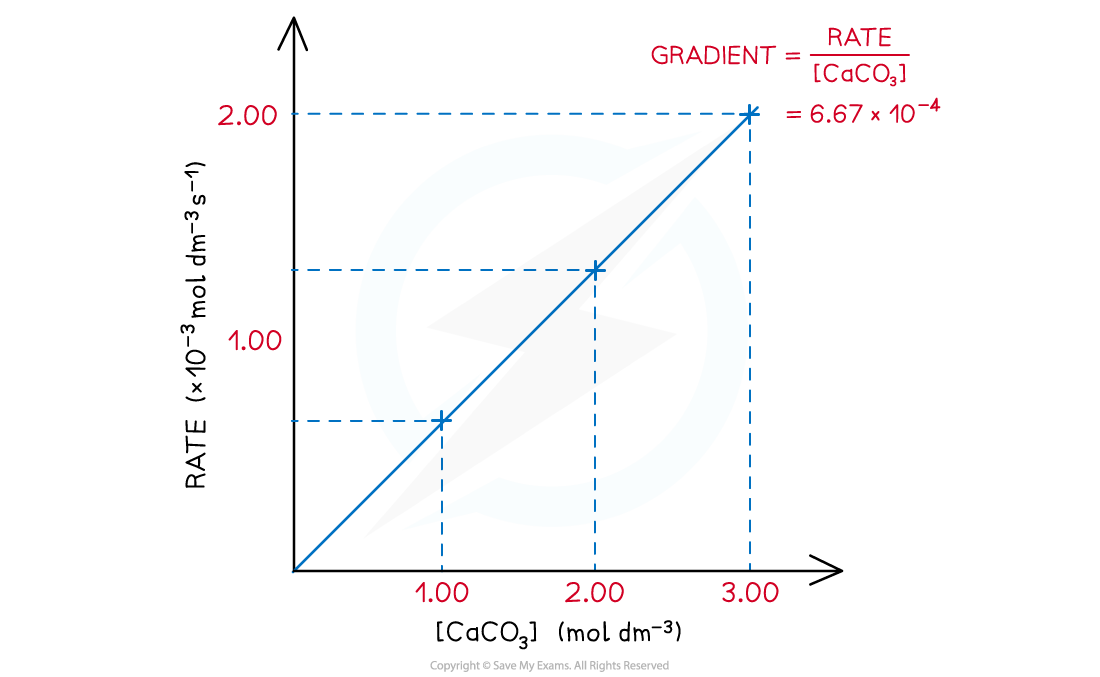
Rate of thermal decomposition of CaCO3?over the concentration of CaCO3
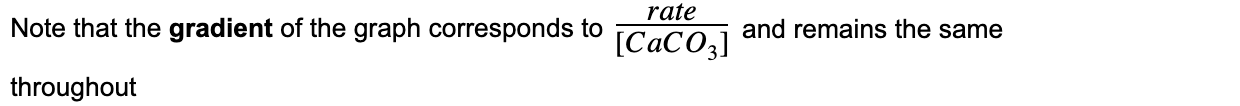
- The rate of reaction for the thermal decomposition of CaCO3?can also be written as:
Rate of reaction =?k?x [CaCO3]
- The?proportionality constant?k?is the gradient of the graph and is also called the?rate constant
- The?rate equation?is the overall expression for a particular reaction without the ‘x’ sign
Rate of reaction =?k?[CaCO3]
- Rate equations can only be determined?experimentally?and cannot be found from the?stoichiometric equation
Rate of reaction =?k?[A]m?[B]n
[A] and [B] = concentrations of reactants
m?and?n?= orders of the reaction
- For example, the?rate equation?for the formation of nitrogen gas (N2) from nitrogen oxide (NO) and hydrogen (H2) is?rate =?k?[NO]2?[H2]
2NO (g) + 2H2?(g) → N2?(g) + 2H2O (g)
rate =?k?[NO]2?[H2]
- As mentioned before, the rate equation of the reaction above cannot be deduced from the stoichiometric equation but can only?experimentally?be determined by:
- Changing the concentration of NO and determining how it affects the rate while keeping [H2] constant
- This shows that the rate is?proportional to?the?square?of [NO]
Rate =?k1?[NO]2
- Then, changing the [H2] and determining how it affects the rate while keeping [NO] constant
- This shows that the rate is?proportional?to [H2]
Rate =?k2?[H2]
- Combining the two equations gives the?overall rate equation?(where?k?=?k1?+ k2)
Rate =?k?[NO]2?[H2]
Order of reaction
- The?order of reaction?shows how the concentration of a reactant affects the rate of reaction
- It is the power to which the concentration of that reactant is raised in the rate equation
- The order of reaction can be 0, 1,2 or 3
- When the order of reaction of a reactant is 0, its concentration is ignored
- The?overall order of reaction?is the sum of the powers of the reactants in a rate equation
- For example, in the following rate equation, the reaction is:
Rate =?k?[NO2]2[H2]
-
- Second-order with respect to NO
- First-order with respect to H2
- Third-order overall (2 + 1)
Half-life
- The?half-life (t1/2)?is the time taken for the concentration of a?limiting reactant?to become half of its initial value
Rate-determining step & intermediates
- The?rate-determining step?is the slowest step in a reaction
- If a reactant appears in the?rate-determining step, then the concentration of that reactant will also appear in the?rate equation
- For example, the rate equation for the reaction below is?rate?=?k?[CH3Br] [OH-]
CH3Br + OH-?→ CH3OH + Br-
-
- This suggests that?both?CH3Br and OH-?take part in the?slow rate-determining step
- This reaction is, therefore, a?bimolecular reaction
- Unimolecular: one species involved in the rate-determining step
- Bimolecular: two species involved in the rate-determining step
- The?intermediate?is derived from substances that react together to form it in the rate-determining step
- For example, for the reaction above the intermediate would consist of CH3Br and OH-

The intermediate is formed from the species that are involved in the rate-determining step (and thus appear in the rate equation)
轉載自savemyexams

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









