- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
CIE A Level Physics復習筆記6.2.2 Elastic Potential Energy
Area under a Force-Extension Graph
- The work done in stretching a material is equal to the force multiplied by the distance moved
- Therefore, the?area under a force-extension graph is equal to the work done?to stretch the material
- The work done is also equal to the?elastic potential energy?stored in the material

Work done is the area under the force - extension graph
- This is true for whether the material obeys Hooke’s law or not
- For the region where the material obeys Hooke’s law, the work done is the area of a right angled triangle under the graph
- For the region where the material doesn’t obey Hooke’s law, the area is the full region under the graph. To calculate this area, split the graph into separate segments and add up the individual areas of each
Loading and unloading
- The force-extension curve for stretching and contraction of a material that has exceeded its elastic limit, but is not plastically deformed is shown below
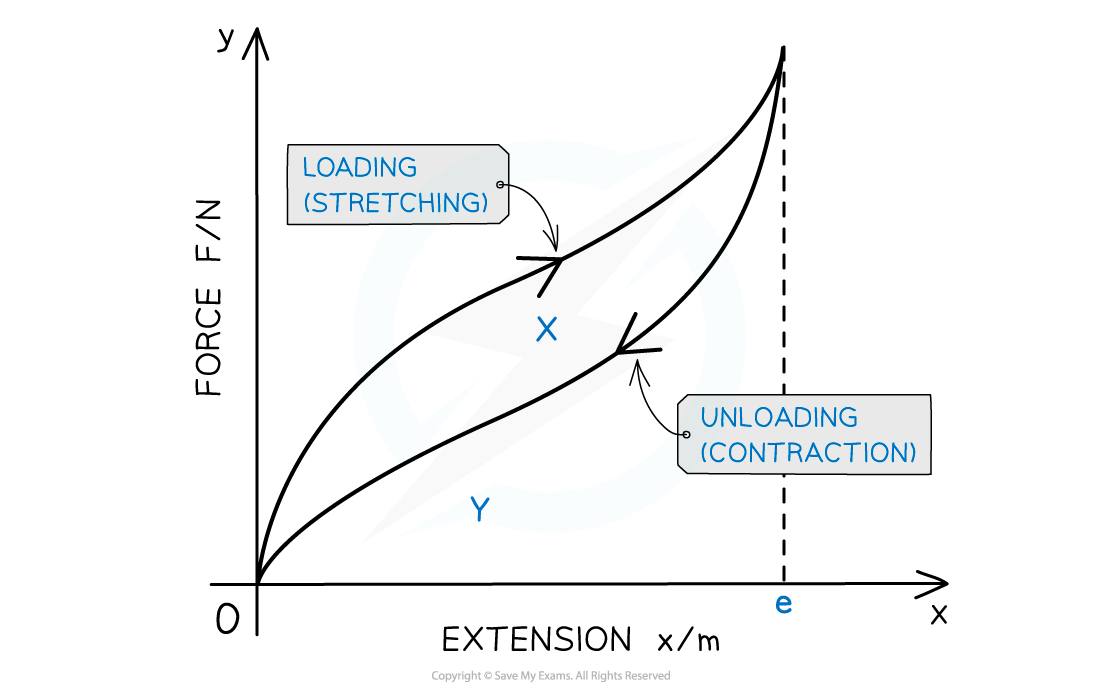
- The curve for contraction is always below the curve for stretching
- The area?X?represents the?net work done?or the?thermal energy?dissipated in the material
- The area?X + Y?is the?minimum energy required?to stretch the material to extension?e
Worked Example
The graph shows the behaviour of a sample of a metal when it is stretched until it starts to undergo plastic deformation.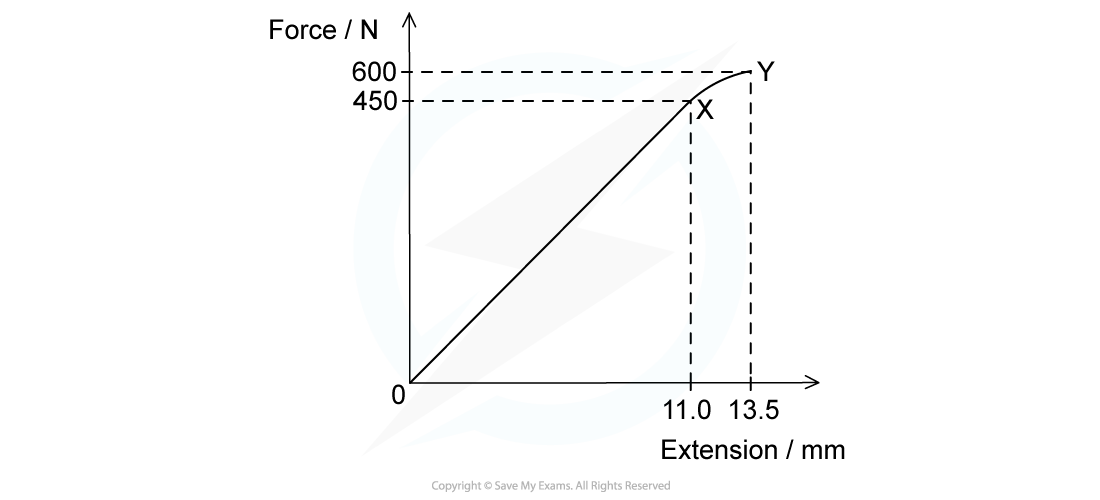
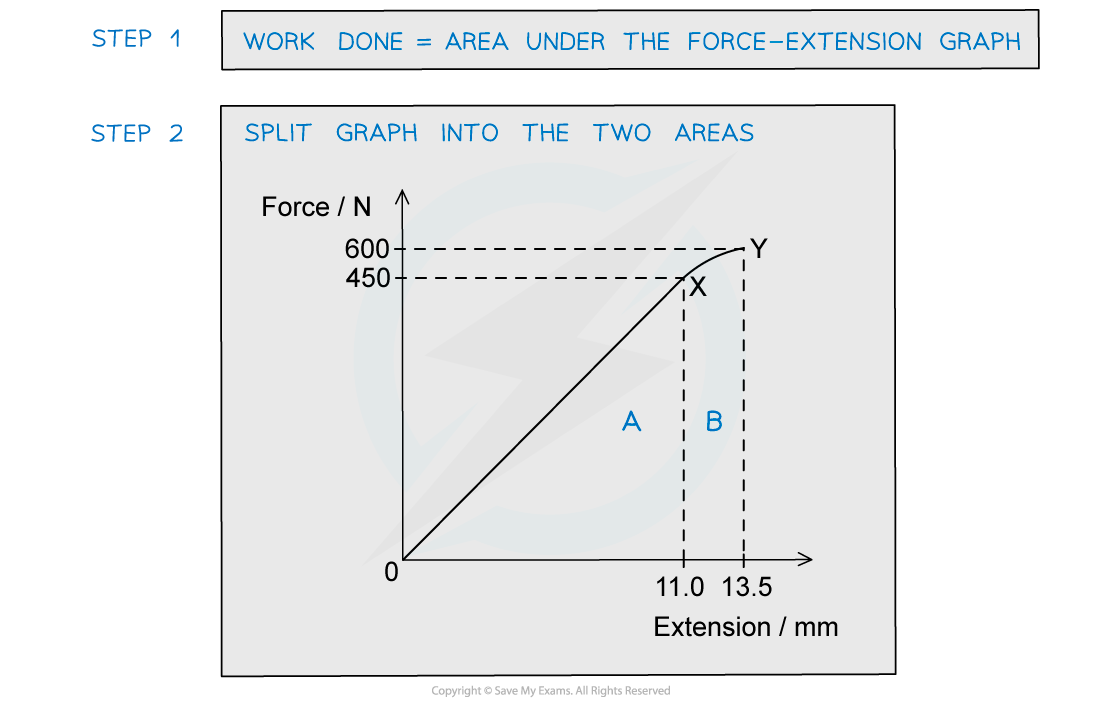
What is the total work done in stretching the sample from zero to 13.5 mm extension?
Simplify the calculation by treating the curve XY as a straight line.

Exam Tip
Make sure to be familiar with the formula for the area of common 2D shapes such as a right angled triangle, trapezium, square and rectangles.
Elastic Potential Energy
- Elastic potential energy is defined as the energy stored within a material (e.g. in a spring) when it is stretched or compressed
- It can be found from the?area under the force-extension graph?for a material deformed within its limit of proportionality
Worked Example
A spring is extended with varying forces; the graph below shows the results.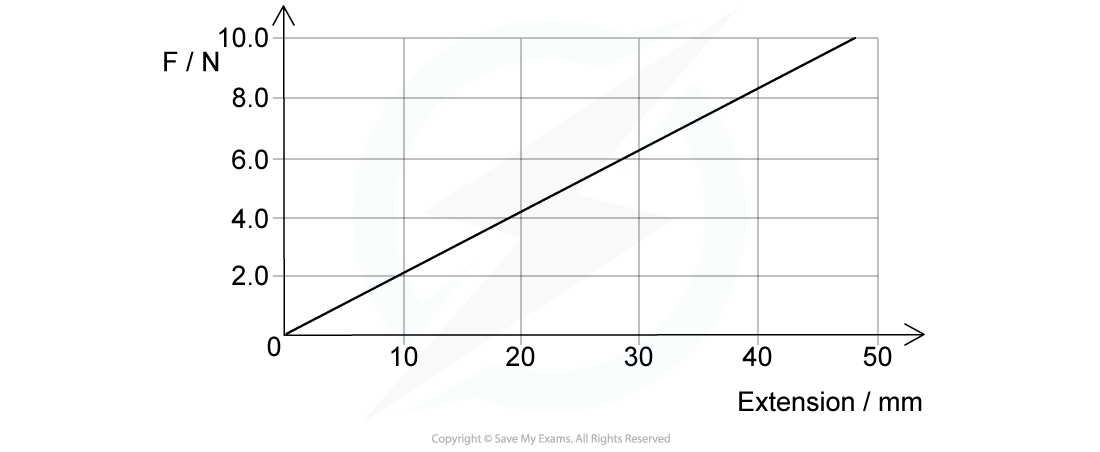
What is the energy stored in the spring when the extension is 40 mm?
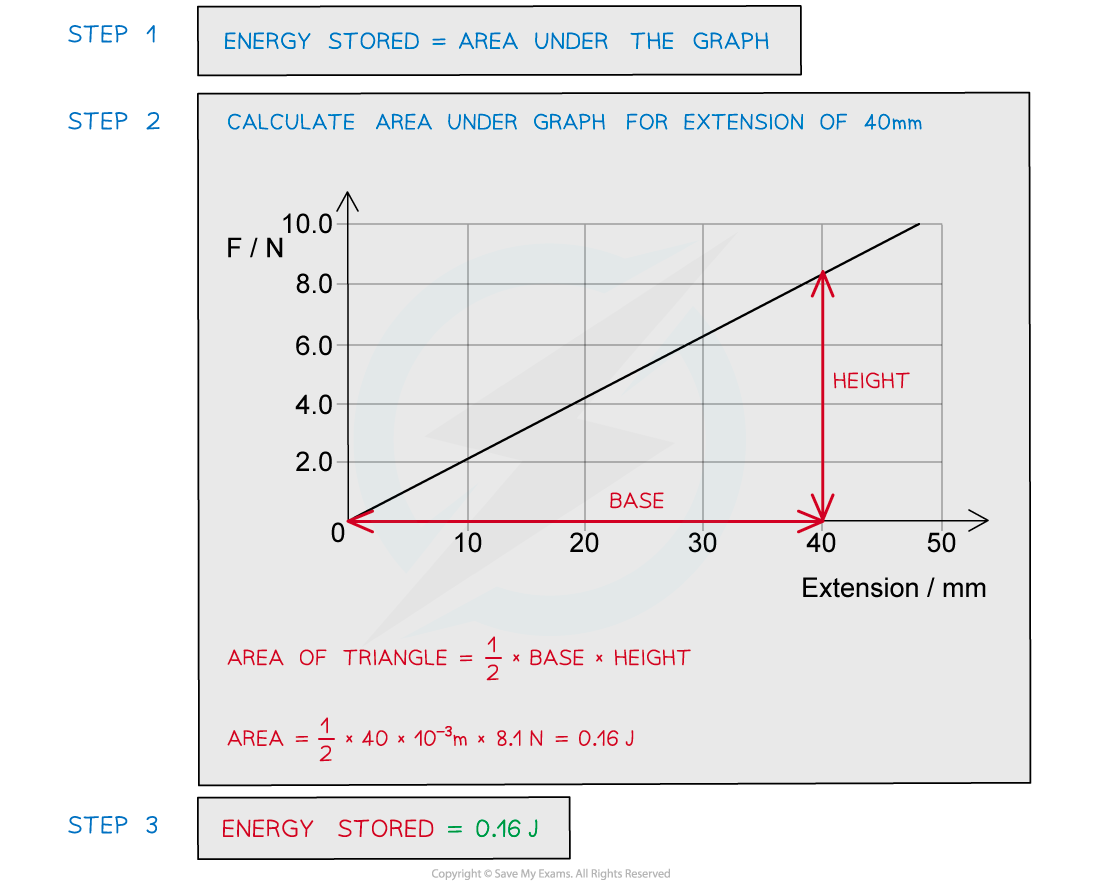
Calculating Elastic Potential Energy
- A material within it’s limit of proportionality obeys Hooke’s law. Therefore, for a material obeying Hooke’s Law, elastic potential energy can be calculated using:

Elastic potential energy can be derived from Hooke’s law
- Where?k?is the?spring constant (N m-1)?and?x?is the?extension (m)
Exam Tip
The formula for EPE = ??kx2?is only the area under the force-extension graph when it is a straight line i.e. when the material obeys Hooke’s law and is within its elastic limit.
轉載自savemyexams

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









