- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
CIE A Level Maths: Pure 3復習筆記8.2.2 Geometry of Complex Addition, Subtraction & Conjugation
Geometry of Complex Addition, Subtraction & Conjugation
What does addition look like on an Argand diagram?
- The?addition?of complex numbers can be shown by the addition of?corresponding column vectors
- If
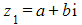 and
and , then
, then
- This can be written as
- If
-
- An alternative is to write
 ?adding the respective real and imaginary parts separately
?adding the respective real and imaginary parts separately
- An alternative is to write
- A complex number
 can be represented by the position vector
can be represented by the position vector
What does subtraction look like on an Argand diagram?
- As with addition we can use knowledge of vectors to represent subtraction of complex numbers
- If
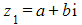 and
and  , then
, then
- This can be written as

- If
-
- An alternative is to write
 subtracting the respective real and imaginary parts separately
subtracting the respective real and imaginary parts separately
- An alternative is to write
What are the geometric representations of complex addition and subtraction?
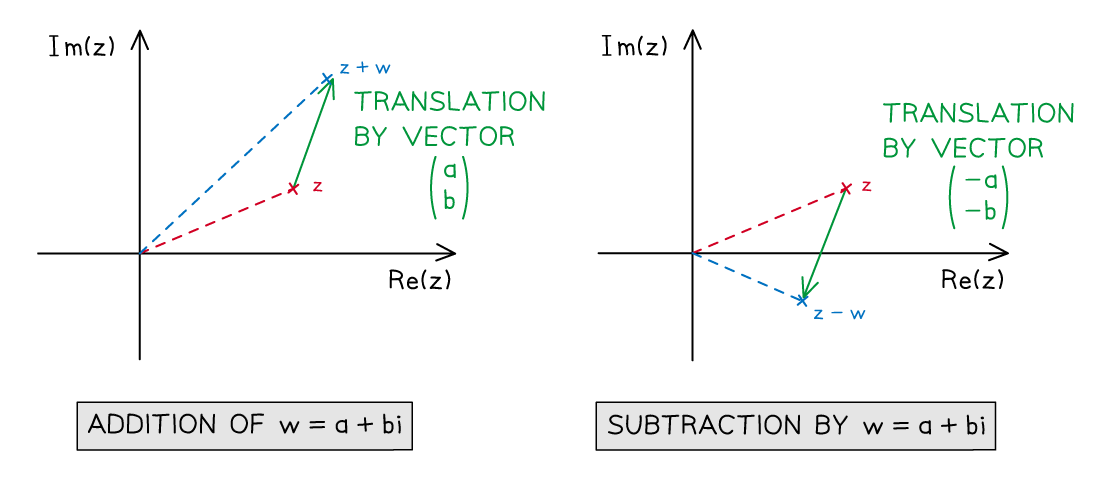
- Let?w?be a given complex number with?real part?a?and?imaginary part?b
- Let?z?be any complex number represented on an Argand diagram
- Adding w to z results in z being translated by vector

- Subtracting w from z results in z being translated by vector

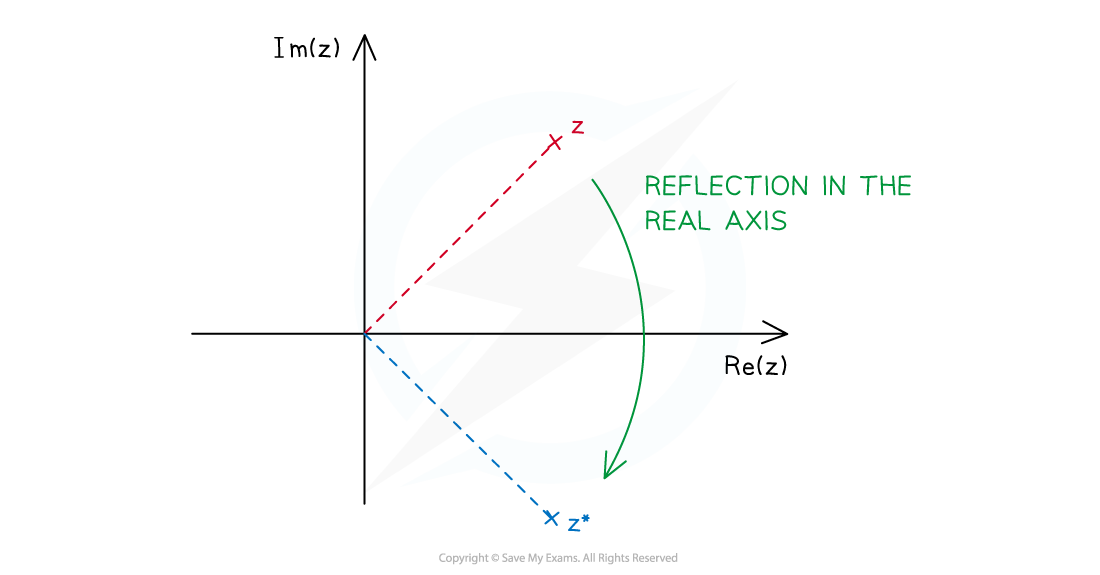
What is the geometric representation of complex?conjugation?
- If we plot?complex conjugate?pairs on an Argand diagram, we notice the points are?reflections?of each other in the?real axis
- Let?z?be any complex number represented on an Argand diagram
- Complex conjugating?z?results in?z?being?reflected?in the real axis
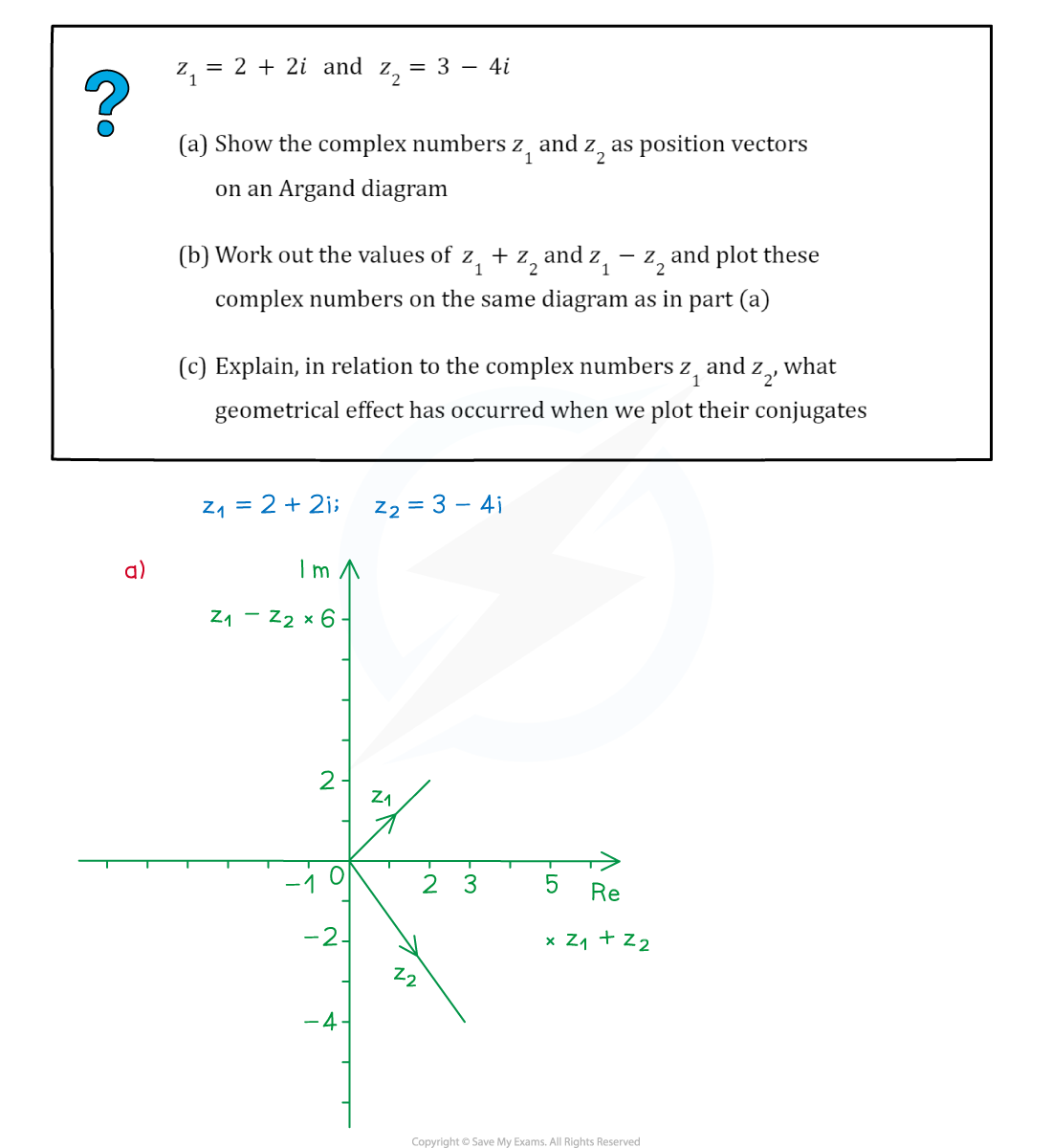
Worked Example

Exam Tip
Read questions carefully; is it asking to plot the complex number as a point or as a vector?
Be extra careful when representing subtraction geometrically, remember that the solution will be a translation of the shorter diagonal of the parallelogram made up by the two vectors.
轉載自savemyexams

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1