邏輯、分析、抽象思維，一起了解“數學”的魅力!

數學是利用符號語言研究數量、結構、變化以及空間模型等概念的一門學科。作為人類思維的表達形式，反映了人們積極進取的意志、縝密周詳的邏輯推理及對完美境界的追求。

雖然不同的傳統學派可以強調不同的側面，然而正是這些互相對立的力量的相互作用，以及它們綜合起來的努力，才構成了數學科學的生命力、可用性和它的崇高價值。

基礎數學知識的運用是個人與團體生活中不可或缺的一部分。其基本概念的精煉早在古埃及、美索不達米亞及古印度的古代數學文本內便可觀見。從那時開始，其發展便持續不斷地有小幅度的進展，直至16世紀的文藝復興時期，因著和新科學發現相作用而生成的數學革新導致了知識的加速，直至今日。

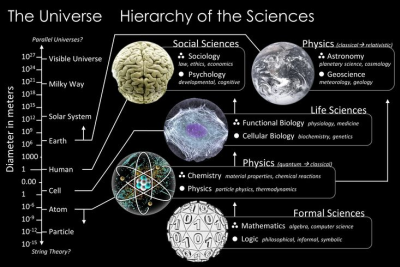
而今日，數學作為基礎的形式科學被廣泛的使用在世界不同的領域上，包括科學、工程、醫學和經濟學等。所以被稱為科學的皇后。

PART 1專業介紹

數學專業的學生研究數字、結構和模式之間的關系。他們的課程范圍從代數到統計學，而且這些概念是相互關聯的。數學系的學生們會學習邏輯、分析、抽象思維和解決問題等技能，這對未來的就業也很有價值。

數學專業的學生會學習代數、微積分、幾何和解決問題所需的不同方程式。他們還學習如何思考并將這一基礎應用于一系列更大、更復雜的問題。

德國數學家卡爾-弗里德里希-高斯稱數學為“科學的女王”，因為它為物理現實帶來了許多啟示。一些學校區分了純數學和應用數學。

描述這兩類數學專業區別的一種方式是，應用數學是將數學用于實際用途，而純數學更像是你可能在電影“Good Will Hunting”或“A Beautiful Mind”中看到的東西。

心靈捕手 Good Will Hunting

換句話說，純數學是對數學本身的研究，沒有外部應用的主要動機，但又并不代表純數學習到的東西無法拿來應用。

PART 2專業分支

純數與應用數學分支

純粹數學

純數-代數 Algebra

01

代數是數學的一個分支，涉及到符號和這些符號的算術運算。這些符號沒有任何固定值，被稱為變量。在我們的現實生活問題中，我們經常看到某些數值在不斷變化。但是，我們一直需要表示這些不斷變化的值。在代數中，這些值通常用符號表示，如x、y、z、p或q，這些符號被稱為變量。此外，這些符號通過加、減、乘、除等各種算術運算進行操作，目的是為了找到這些數值。

代數方程的表示

簡單地來說，代數就是研究運算系統的學科，是一切關于計算的基礎，如果只是從表面來看，代數就是解方程，解的還是代數方程。不過代數遠遠不止如此，它更像是一門語言，給數學家用的語言，用以描述其他的數學事物，并且在研究量子力學的基本粒子，在考察剛體性質和晶體結構（群表示），在分析經濟模式，在制造現代計算機等方面都是十分有用的。

純數-數理邏輯 Mathematical Logic

02

數理邏輯是數學的分支，研究的是一些非常專門的問題。比如“決定性公理在ZF系統中的協調性與何種大基數等價”。這些知識對于日常的一般事物的“邏輯”分析沒有幫助。就像一個代數幾何專家不會更擅長辯論一樣。

數理邏輯，其實是在用經典概念的內涵表示進行計算，這個經典概念的內涵表示就是命題，而命題必須是可以判斷二值真假的陳述句這就是問題的根源實際生活經驗中，大多數概念都是不能用命題表示的為了補足這個問題，于是又有了概念的原型理論、樣例理論等等但數理邏輯依舊發揮著不可取代的作用像是蘊含式這樣違背人類直覺的東西，其實本來就不是設計給人看的，而是設計給機器看的，所以學好數理邏輯，也是為了計算機算法做鋪墊。

數理邏輯與算法的聯系

純數-拓撲學 Topology

03

拓撲描述的是局部形變下的不變性。舉個例子，對于拓撲學家來說，咖啡杯和面包圈沒什么區別。因為只要圖形的閉合性質不被破壞，在拓撲學上它們就都是等價的。

拓撲學家晨間例行公事

現代數學中有太多的結構都離不開拓撲，拓撲學的基本內容已經成為現代數學工作者的常識，是現代數學的基本語言。

拓撲學的重要性，體現在它與其他數學分支、其他學科的相互作用，就像拓撲學在泛函分析（度量空間，Hilbert空間等都是拓撲空間）、實分析、群論、微分幾何、微分方程等其他許多數學分支中都有非常廣泛的應用。