- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
2012COMC加拿大數學公開賽真題免費下載
歷年 Canadian Open Mathematics Challenge加拿大數學公開賽
真題與答案下載
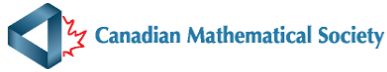
翰林國際教育全網首發
力爭超快速發布最全資料
助你在升學路上一帆風順
為你
千千萬萬遍
2012 COMC真題免費下載
共計2.5小時考試時間
此套試卷由三部分題目組成
4題簡答題,每題4分
4題挑戰題,每題6分
4題解答題,每題10分
共計12題,滿分80分
不可使用任何計算器
完整版下載鏈接見文末
部分真題預覽:
Part A Introductory Questions:
Question A3)Let ABCDEF be a hexagon all of whose sides are equal in length and all of whose angles are equal. The area of hexagon ABCDEF is exactly r times the area of triangle ACD. Determine the value of r.
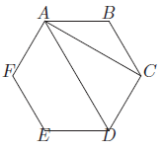
Question A4)Twelve different lines are drawn on the coordinate plane so that each line is parallel to exactly two other lines. Furthermore, no three lines intersect at a point. Determine the total number of intersection points among the twelve lines.
Part B Challenging Questions:
Question B1)Twelve different lines are drawn on the coordinate plane so that each line is parallel to exactly two other lines. Furthermore, no three lines intersect at a point. Determine the total number of intersection points among the twelve lines.
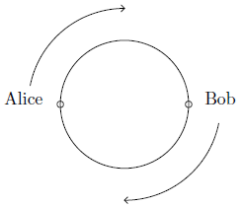
When they meet for the first time, Alice has completed exactly 30 laps. Determine all possible values of t.
Part C Long-form Proof Problems:
Question C2)We fill a 3 × 3 grid with 0s and 1s. We score one point for each row, column, and diagonal whose sum is odd.
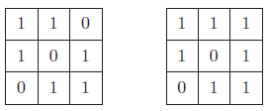
For example, the grid on the left has 0 points and the grid on the right has 3 points.
- Fill in the following grid so that the grid has exactly 1 point. No additional work is required. Many answers are possible. You only need to provide one.

- Determine all grids with exactly 8 points.
- Let E be the number of grids with an even number of points, and O be the number of grids with an odd number of points. Prove that E = O.
完整版真題下載鏈接請注冊或登錄后查看
文件為PDF格式
推薦使用電腦下載
2012 COMC加拿大數學奧賽完整版答案免費下載
請持續關注,稍后更新
翰林學員全站資料免費打包下載,專享高速下載通道。
[vc_btn title="查看更多COMC加拿大數學奧賽相關詳情" color="primary" align="center" i_icon_fontawesome="fa fa-globe" css_animation="zoomIn" button_block="true" add_icon="true" link="url:http%3A%2F%2Fwww.linstitute.net%2Farchives%2F99767||target:%20_blank|"]

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









