2008COMC加拿大數學公開賽真題免費下載

歷年 Canadian Open Mathematics Challenge加拿大數學公開賽

真題與答案下載

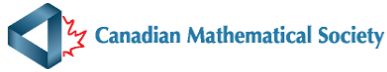
翰林國際教育全網首發

力爭超快速發布最全資料

助你在升學路上一帆風順

為你

千千萬萬遍

2008 COMC真題免費下載

共計2.5小時考試時間

此套試卷由兩部分題目組成

Part A共8題，每題5分

Part B共4題，每題10分

共計12題，滿分80分

不可使用任何計算器

完整版下載鏈接見文末

部分真題預覽：

Part A :

4)In the diagram, D is on AB and E is on AC with DE parallel to BC. Also, DE = 1, BC = 6, AE = x, and EC = x² + 4. Determine all possible values of x.

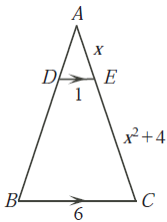
6)Rectangle ABCD intersects a circle at points E, F,G, and H, as shown. If AH = 4, HG = 5 and BE = 3, determine the length of EF.

7)A star is placed in the bottom right corner square of a 3 × 3 grid, as shown. A fair coin is flipped repeatedly. Each time that the coin shows heads, the star is moved one space upwards; each time that the coin shows tails, the star is moved one space to the left. (The star may move off the grid.) Determine the probability that the star reaches the top left corner square of the grid.

Part B :

4)A triangle is called automedian if its three medians can be used to form a triangle that is similar to the original triangle.

1. Show that the triangle with sides of length 7, 13 and 17 is automedian.
2. ΔABC has side lengths AB = c, AC = b and BC = a, with a < b < c. If ΔABC is automedian, prove that a2 + c2 = 2b2.
3. Determine, with proof, an infinite family of automedian triangles with integer side lengths, such that no two of the triangles in the family are similar.

完整版真題資料可以底部二維碼免費領取↓↓↓

[vc_btn title="查看更多COMC加拿大數學奧賽相關詳情" color="primary" align="center" i_icon_fontawesome="fa fa-globe" css_animation="zoomIn" button_block="true" add_icon="true" link="url:http%3A%2F%2Fwww.linstitute.net%2Farchives%2F99767||target:%20_blank|"]