初中幾何之勾股定理的六種常見(jiàn)證明方法

勾股定理作為幾何計(jì)算中的重要定理，其地位無(wú)可撼動(dòng)。它不僅在數(shù)學(xué)中占據(jù)重要位置，也是許多實(shí)際問(wèn)題解決的基礎(chǔ)。隨著歷史的發(fā)展，勾股定理的證明方法也不斷豐富，至今已有近十種之多。本文將為大家詳細(xì)介紹六種常見(jiàn)的證明方法，幫助初學(xué)者深入理解勾股定理的本質(zhì)。

什么是勾股定理？

勾股定理是指在直角三角形中，直角兩邊的平方和等于斜邊的平方。用公式表示為：

其中，$a$?和?$b$?為直角邊，$c$?為斜邊。理解這一關(guān)系是學(xué)習(xí)幾何的重要基礎(chǔ)。

六種常見(jiàn)證明方法

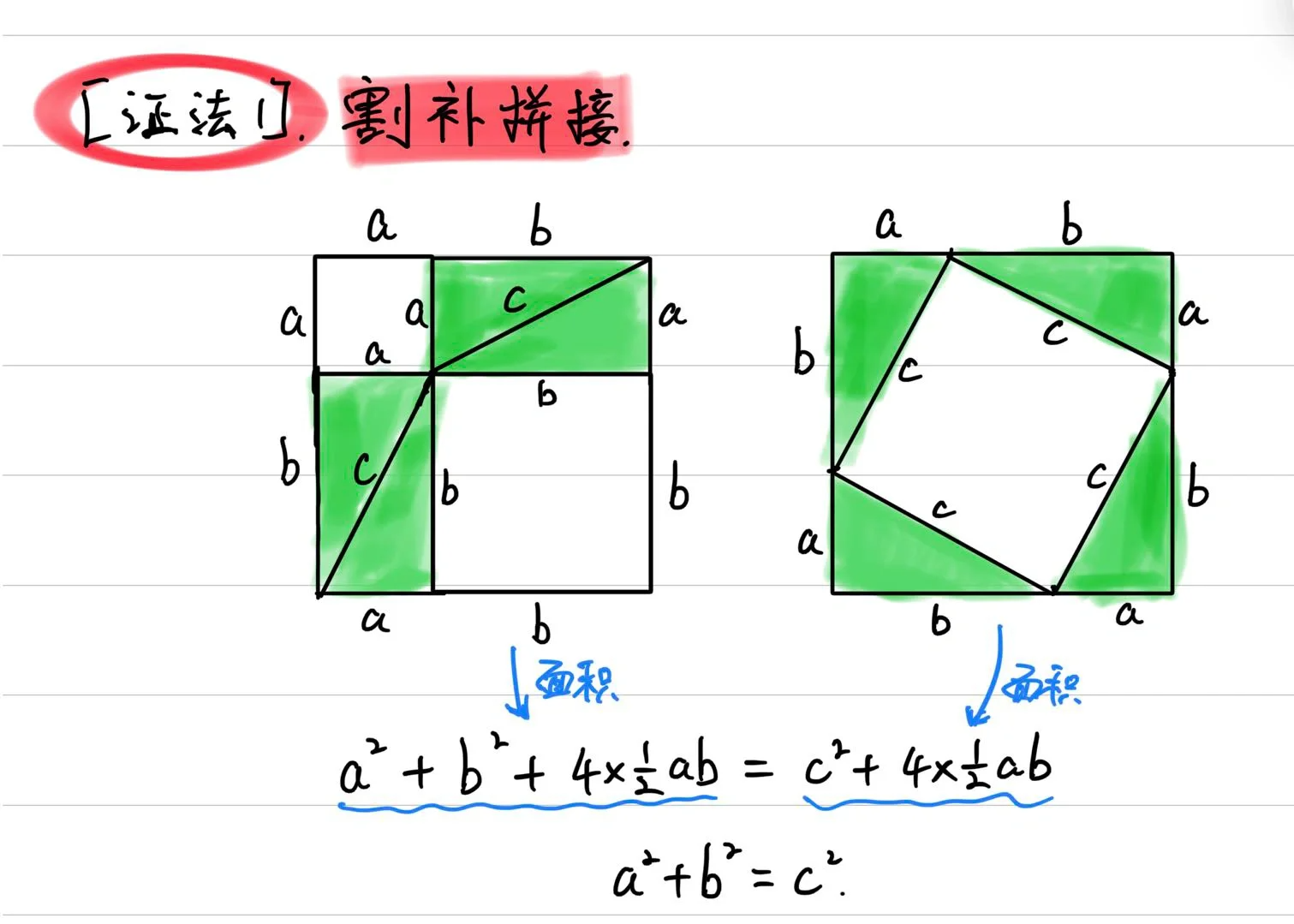
1. 割補(bǔ)拼接法

割補(bǔ)拼接法是通過(guò)將直角三角形分割成不同的部分，重新拼接來(lái)證明勾股定理。這種方法直觀易懂，適合初學(xué)者。具體步驟如下：

• 將直角三角形的兩條直角邊分別延長(zhǎng)，形成一個(gè)大正方形。
• 在這個(gè)大正方形內(nèi)部，拼接出兩個(gè)小正方形，分別對(duì)應(yīng)于直角邊的平方。
• 通過(guò)計(jì)算大正方形和小正方形的面積關(guān)系，得出勾股定理的結(jié)論。

2. 內(nèi)弦圖法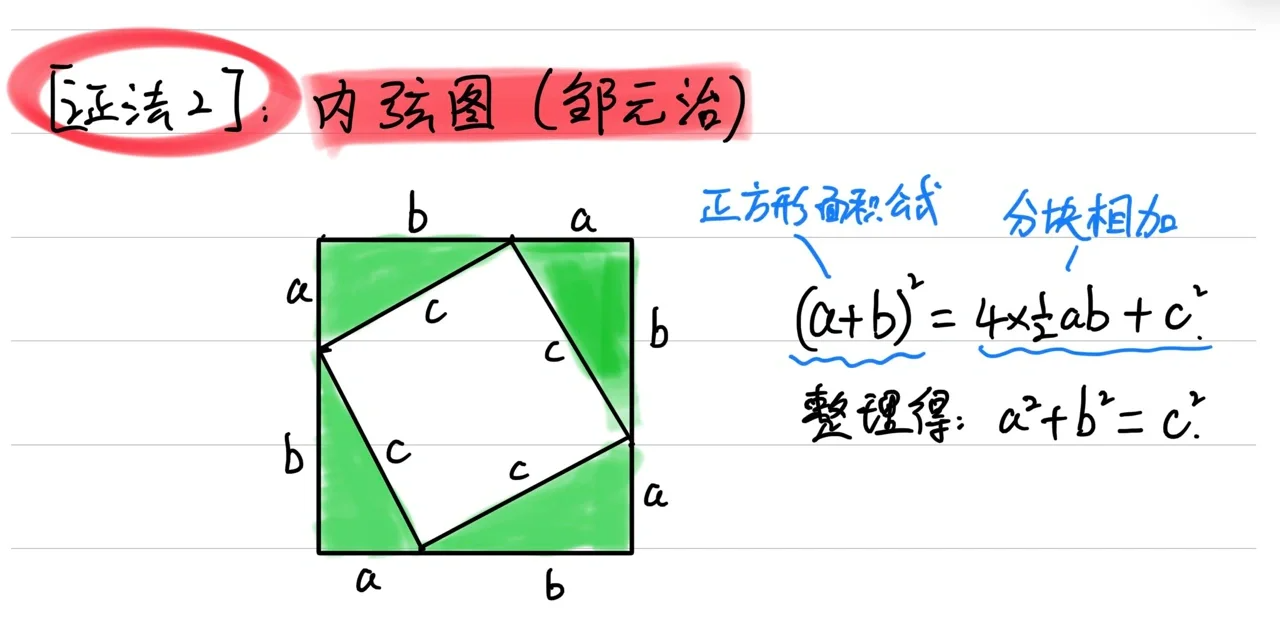

內(nèi)弦圖法利用幾何圖形的對(duì)稱性進(jìn)行證明。具體步驟為：

• 在直角三角形內(nèi)部畫(huà)出一個(gè)內(nèi)切圓。
• 通過(guò)分析內(nèi)切圓與三角形各邊的關(guān)系，推導(dǎo)出面積的變化。
• 最終得出直角邊平方和等于斜邊平方的結(jié)論。

3. 外弦圖法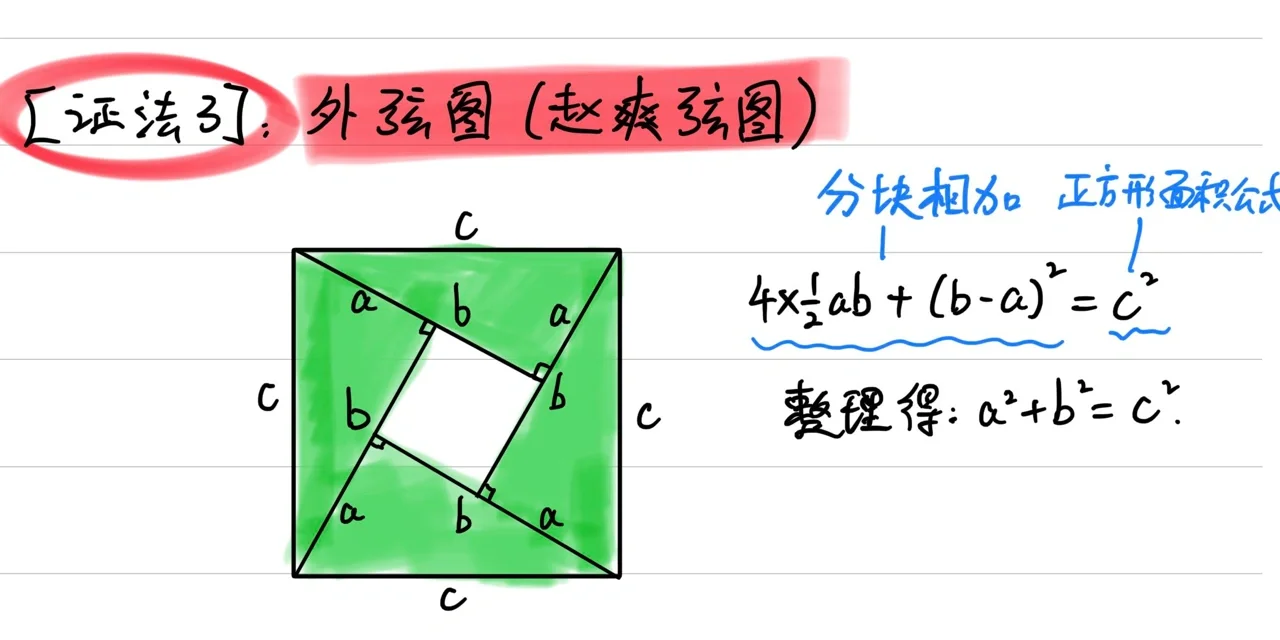

外弦圖法與內(nèi)弦圖法相對(duì)，通過(guò)外部圖形的構(gòu)建進(jìn)行證明。步驟如下：

• 在直角三角形外部構(gòu)建一個(gè)外接圓。
• 通過(guò)分析外接圓的弦長(zhǎng)與三角形各邊的關(guān)系，推導(dǎo)出面積之間的關(guān)系。
• 最終得出勾股定理的結(jié)論。

4. 總統(tǒng)證法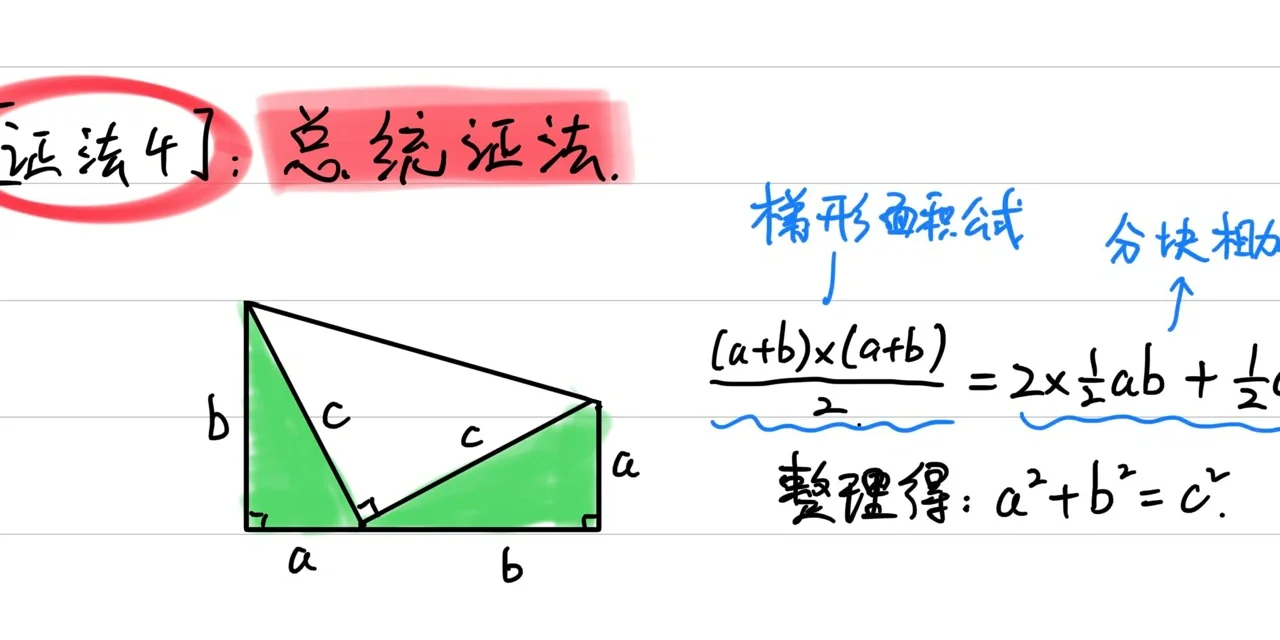

總統(tǒng)證法以其獨(dú)特的幾何構(gòu)造而聞名。具體步驟為：

• 選取一個(gè)直角三角形，在其周?chē)鷺?gòu)建一個(gè)大的正方形。
• 將直角三角形的三個(gè)頂點(diǎn)分別與正方形的邊相連，形成新的圖形。
• 通過(guò)計(jì)算新圖形的面積，推導(dǎo)出勾股定理的關(guān)系。

5. 青朱出入圖法

青朱出入圖法通過(guò)圖形的動(dòng)態(tài)變化進(jìn)行證明。具體步驟為：

• 在直角三角形中引入青朱的概念，通過(guò)圖形的變化展示面積的轉(zhuǎn)化。
• 通過(guò)對(duì)比不同形狀的面積，得出直角邊平方和等于斜邊平方的結(jié)論。

6. 歐幾里得證法

歐幾里得證法是最經(jīng)典的證明方法之一，步驟如下：

• 通過(guò)構(gòu)造一個(gè)正方形，并在其內(nèi)部放置直角三角形。
• 通過(guò)對(duì)比正方形的面積與直角三角形的面積，推導(dǎo)出勾股定理的結(jié)論。

結(jié)語(yǔ)

勾股定理的多種證明方法不僅豐富了我們的數(shù)學(xué)知識(shí)，也幫助我們更好地理解幾何圖形之間的關(guān)系。初學(xué)者在學(xué)習(xí)過(guò)程中，理解這些證明方法的本質(zhì)，即“幾何圖形面積之間的變形轉(zhuǎn)化”，將有助于更深入掌握勾股定理。

希望今天的分享能對(duì)大家的學(xué)習(xí)有所幫助。如果你喜歡這篇文章，歡迎關(guān)注、點(diǎn)贊和轉(zhuǎn)發(fā)，讓我們一起在數(shù)學(xué)的道路上不斷進(jìn)步！