從勾股定理的不同證明方法看代數與幾何的比較

勾股定理的多種證明方法各具特色，尤其是歐幾里得的幾何證明方法與代數證明方法之間的對比，展現了數學思維的多樣性。本文將深入探討這兩種證明方法的特點及其在學習過程中的應用。

歐幾里得的幾何證明方法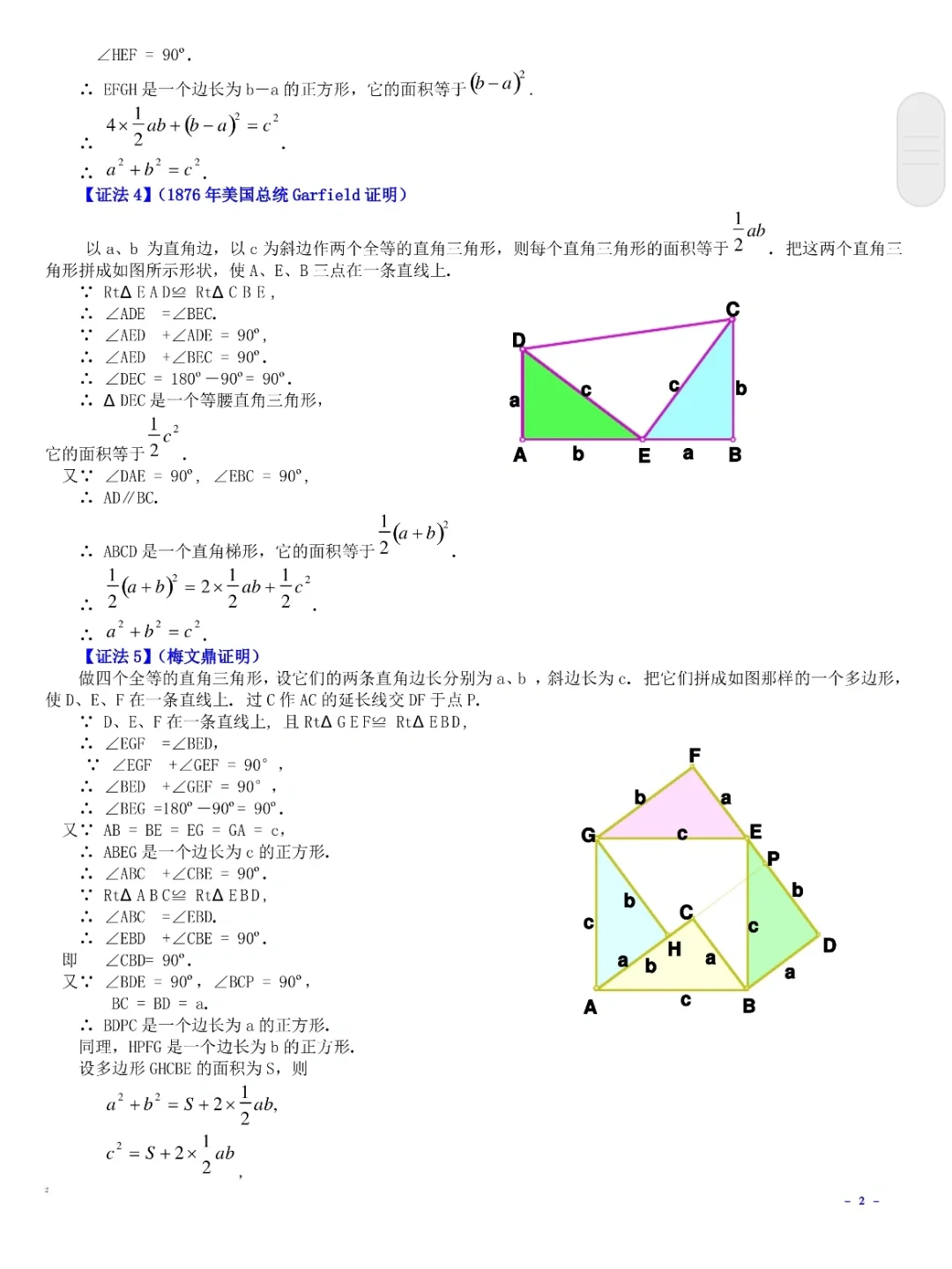

歐幾里得的證明方法以其嚴謹性和邏輯性著稱，主要依賴于幾何圖形的性質。其基本思路是通過尋找相等的線段和角，來證明三角形的全等性，并由此建立等量關系。具體步驟包括：

• 構造圖形：在直角三角形中添加輔助線，形成新的幾何圖形。
• 證明全等：使用邊角邊（SAS）、角邊角（ASA）等全等條件，證明所構造的三角形全等。
• 建立等量關系：通過全等三角形的性質，得出勾股定理的結論。

這種方法雖然嚴謹，但在輔助線的構造上往往需要靈活的思維和豐富的幾何直覺。初學者在學習過程中，常常會遇到難以想到合適輔助線的困擾，這就需要較高的空間想象力和邏輯推理能力。

代數證明方法的簡單明了

相比之下，代數證明方法如趙爽弦圖和總統法則則顯得簡單明了。其核心在于設未知量并尋找等量關系，具體步驟如下：

• 設未知數：在證明過程中，設定多個未知數，構建代數方程。
• 尋找等量關系：通過已知條件和設定的未知數，建立等量關系，形成方程。
• 代數化簡：通過基本的代數運算，將方程化簡，最終得出勾股定理。

代數證明方法的優勢在于其直接性和靈活性。只要敢于設定未知數，思路就會變得清晰明了。代數方法不僅降低了思維的復雜度，還能幫助學生在解題過程中建立自信。

結論

從勾股定理的不同證明方法中，我們可以看到幾何與代數的各自特點。歐幾里得的幾何證明方法強調邏輯嚴謹性和空間想象力，而代數證明方法則以其簡單明了的思路吸引人。對于初學者而言，掌握代數證明方法可以為理解幾何概念打下良好的基礎，同時也能增強解決問題的信心。

希望通過對這兩種證明方法的比較，能夠幫助學生更好地理解勾股定理，并在學習過程中找到適合自己的思維方式。