ICM實用模型及例題（D題）

國內常說的美國大學生數學建模學術活動，其實是由兩種類型的學術活動組成，MCM即Mathematical Contest in Modeling，直譯為數學建模學術活動，和ICM即The Interdisciplinary Contest in Modeling，直譯為交叉學科建模學術活動，兩者名稱不同，題目的風格有較大的差異。ICM學術活動題目更開放，問題更“大”，更宏觀，篇幅較長，往往是全球范圍內共同關心的問題，因此一般不依賴特定的文化背景或生活習慣，近幾年ICM學術活動要求論文正文部分不超過20頁。

D題：operations?research/network science 問題簡介

自2016年開始，ICM由原來的一道題增至三道題，一般為D題、E題、F題，分別為operations research/network science、environmental science和policy這三種類型。首先我們介紹一下D題也就是operations research/network science這個部分。

D題一般是運籌學和網絡科學的問題，所用到模型、算法、軟件比較集中，有章可循。運籌學是以整體最優為目標，從系統的觀點出發，力圖以整個系統最佳的方式來解決該系統各部門之間的利害沖突的一門學科。它對所研究的問題求出最優解，尋求最佳的行動方案，所以它也可看成是一門優化技術，提供的是解決各類問題的優化方法。

而網絡科學是近幾年的一個熱門研究領域，比如著名的“哥尼斯堡七橋”問題，其實就是網絡科學較早的實際問題，歐拉在1736年用抽象分析法解決了這個問題，這也使歐拉成為圖論〔及拓撲學〕的創始人。如果對求解最優解問題和圖論問題感興趣，或者對這些領域的相關知識和軟件都比較熟悉，選題時可以重點關注D題。今天我們首先介紹這道題常用的四種數學模型，分別是Programming數學規劃、complex network復雜網絡、Queuing排隊論和Clustering聚類分析。

Programming 數學規劃

一般地，優化模型可以表述如下：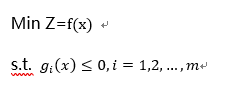

這是一個多元函數的條件極值問題，其中 x = [ x 1 , x 2 , … , x n ]。許多實際問題歸結出的這種優化模型，但是其決策變量個數 n 和約束條件個數 m 一般較大，并且最優解往往在可行域的邊界上取得，這樣就不能簡單地用微分法求解，數學規劃就是解決這類問題的有效方法。三要素：決策變量、目標函數、約束條件適用場景：

1.實際對象特征間及特征與環境間的交互不存在非線性關系的優化問題

2.需利用非線性刻畫對限制條件或當前局勢進行描述的優化問題

3.決策控制域離散且域中相鄰兩個元素間測度相等的優化問題

4.需在多個目標間進行權衡達到整體局勢最優的優化問題

5.以時間劃分階段的動態過程的優化問題

建模步驟：

Step 1. 尋求決策，即回答什么？必須清楚，無歧義。

Step 2. 確定決策變量

第一來源：Step 1的結果，用變量固定需要回答的決策

第二來源：由決策導出的變量（具有派生結構）

其它來源：輔助變量（聯合完成更清楚的回答）

Step 3. 確定優化目標

用決策變量表示的利潤、成本等。

Step 4. 尋找約束條件

決策變量之間、決策變量與常量之間的聯系。

第一來源：需求；

第二來源：供給；

其它來源：輔助以及常識。

Step 5. 構成數學模型

將目標以及約束放在一起，寫成數學表達式。常見類型：

線性規劃 （目標函數及約束條件均為線性函數）

整數規劃 （決策變量部分或全部被限制為整數）

多目標規劃 （具有多于一個的目標函數）

動態規劃（把多階段過程轉化為一系列單階段問題，逐個求解）

complex network 復雜網絡

在我們的現實生活中，許多復雜系統都可以建模成一種復雜網絡進行分析，比如常見的電力網絡、航空網絡、交通網絡、計算機網絡以及社交網絡等等。具有自組織、自相似、吸引子、小世界、無標度中部分或全部性質的網絡稱之為復雜網絡，言外之意，復雜網絡就是指一種呈現高度復雜性的網絡。

適用場景l社團檢測：潛在客戶挖掘、關聯群體風險分析等；l網絡中心性分析：網頁排名（PageRank），供應鏈核心企業識別，信息傳播樞紐節點識別等；網絡傳播預測：流行病傳播，金融風險傳播，輿論傳播；

網絡關系滲透：節點之間的關系（三度影響）；

關聯交易分析及投融資黑洞：虛假交易，擔保圈分析等。

基本概念

l節點、邊

l關聯與鄰接

l度 k、平均度 <k>

l節點的度分布p(k)

l最短路徑與平均路徑長度（Dijkstra算法）

常用網絡

ER模型：Erd?s和Rényi （ER）最早提出隨機網絡模型并進行了深入研究，他們是用概率統計方法研究隨機圖統計特性的創始人。給定N個節點，沒有邊，以概率p用邊連接任意一對節點，用這樣的方法產生一隨機網絡。

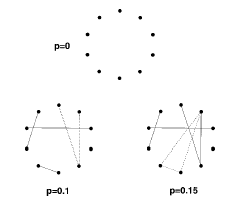
節點的度分布：平均值為的泊松分布小世界模型: 為了描述從一個局部有序系統到一個隨機網絡的轉移過程，Watts和 Strogatz（WS）提出了一個新模型，通常稱為小世界網絡模型。WS模型始于一具有N個節點的一維網絡，網絡的節點與其最近的鄰接點和次鄰接點相連接，然后每條邊以概率p重新連接。

約束條件為節點間無重邊，無自環。當p等于0時，對應于規則圖。兩個節點間的平均距離<L>線性地隨N增長而增長，集聚系數大。當p等于1時，系統變為隨機圖。 <L>對數地隨N增長而增長，且集聚系數隨N減少而減少。

在p等于（0，1）區間任意值時，<L>約等于隨機圖的值，網絡具有高度集聚性---小世界效應。

無標度(Scale-free)網絡: 無標度模型由Albert-László Barabási和Réka Albert在1999年首先提出，現實網絡的無標度特性源于眾多網絡所共有的兩種生成機制：（ⅰ）網絡通過增添新節點而連續擴張； （ⅱ）新節點擇優連接到具有大量連接的節點上。

具有性質：度分布呈冪率分布、中樞節點出現、魯棒性、脆弱性。

Queuing 排隊論

面對擁擠現象，人們總是希望盡量設法減少排隊，通常的做法是增加服務設施，但是增加的數量越多，人力、物力的支出就越大，甚至會出現空閑浪費，如果服務設施太少，顧客排隊等待的時間就會很長，這樣對顧客會帶來不良影響。顧客排隊時間的長短與服務設施規模的大小，就構成了設計隨機服務系統中的一對矛盾。

如何做到既保證一定的服務質量指標，又使服務設施費用經濟合理，恰當地解決顧客排隊時間與服務設施費用大小這對矛盾。這就是隨機服務系統理論——排隊論所要研究解決的問題。適用場景排隊論里把要求服務的對象統稱為“顧客”,而把提供服務的人或機構稱為“服務臺”或“服務員”。不同的顧客與服務組成了各式各樣的服務系統。顧客為了得到某種服務而到達系統、若不能立即獲得服務而又允許排隊等待，則加入等待隊伍，待獲得服務后離開系統。

主要流程

l? 確定時間分布（到達時間和服務時間）

l? 研究系統理論分布的概率特征

l? 研究系統狀態的概率

l? 求解概率分布和特征數

l? 指標優化與運營優化

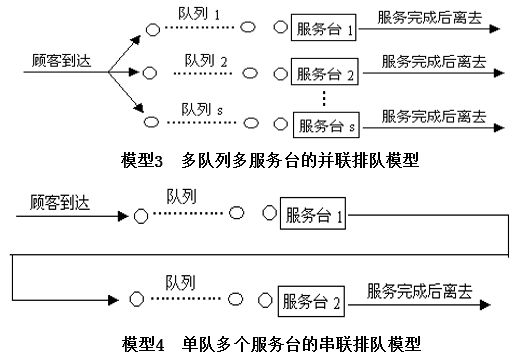
排隊模型

根據顧客到達和服務臺數，排隊過程可用下列模型表示：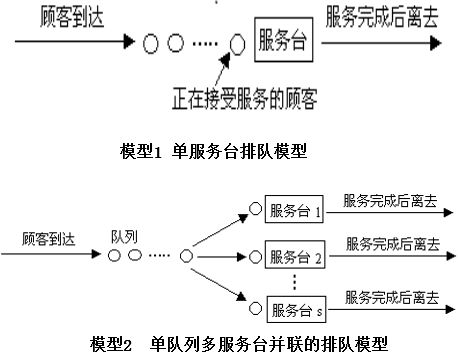

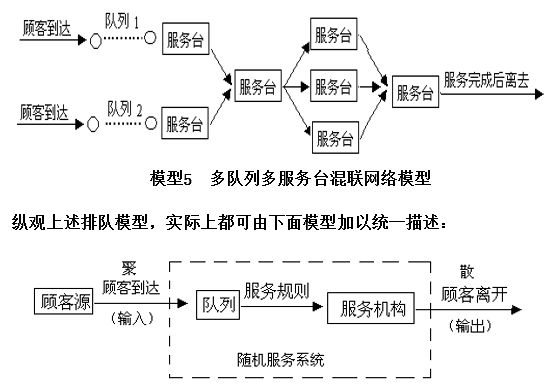
Clustering 聚類分析

聚類分析顧名思義是一種分類的多元統計分析方法。按照個體或樣品的特征將它們分類，使同一類別內的個體具有盡可能高的同質性，而類別之間則應具有盡可能高的異質性。

常見類型l劃分

聚類? k-means、k-medoids、k-modes、k-medians、kernel k-mea

層次聚類 Agglomerative 、divisive、BIRCH、ROCK、Chameleo

密度聚類 DBSCAN、OPTICS

網格聚類? STING

模型聚類? GMM

圖聚類? Spectral Clustering（譜聚類）偏最小二乘回歸

主要流程

1.對數據進行變換處理；（不是必須的，當數量級相差很大或指標變量具有不同單位時是必要的）

2.構造n個類，每個類只包含一個樣本；

3.計算n個樣本兩兩間的距離；

4.合并距離最近的兩類為一新類；

5.計算新類與當前各類的距離，若類的個數等于1，轉到6；否則回4；

6.畫聚類圖；

7.決定類的個數，從而得出分類結果。指標優化與運營優化
常見距離度量