AMC系列 | 第二講：符合勾股定理的所有整數，都畫在坐標系中是什么樣？

AMC美國數學學術活動系列將連載12期，根據AMC10/12體系，來講解其涉及到的各個知識點，并為公立學校和國際學校的學生提供中英文對照。本期要點1.勾股定理的歷史2.勾股定理的證明3.勾股定理的應用4.純代數層面的勾股定理

先來做個小練習：已知一個直角三角形兩個斜邊長分別是2和3，問斜邊長為多少？ok，現在你腦子里一定在想平方、開方的事了。可你有沒有想過，為什么要平方和開方。三角形斜邊長的平方為什么就是兩個直角邊的平方和？誰先發現這個有趣性質的？

這就得從勾股定理這個名字講起，古人把直角三角形較小的直角邊叫做勾，較長的直角邊叫做股，斜邊叫做弦，描述三者關系的定理就叫勾股定理。早在春秋時期，它就被中國人發現，后記載于《九章算數》。

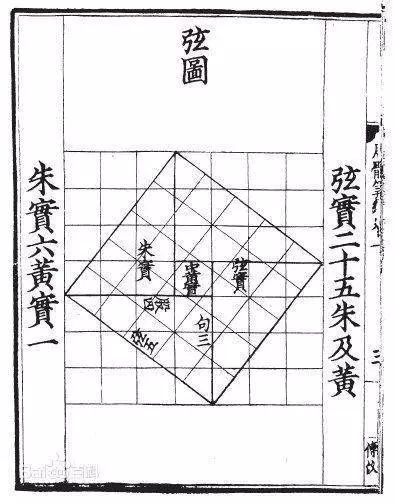
（上圖：勾三股四弦五）客觀的說，雖然中國人早于西方發現這一性質，但最先將此性質推廣到任意直角三角形并予以證明的是古希臘數學家畢達哥拉斯 (Pythagoras) ，因此這個定理也叫做畢達哥拉斯定理 (Pythagorean Theorem) ，我們常見到的黃金分割、整數、分數這些概念也源于畢達哥拉斯學派

這個定理怎么證明呢？中國古人的證法是用割補法，僅用正方形面積公式就能證明：

勾股定理新的證明方法不斷被人想出，有趣的是，有個叫加菲爾德的人在用他的方法證出本定理5年之后，成為美國第20任總統，所以人們又稱這個證法為“總統證法”。

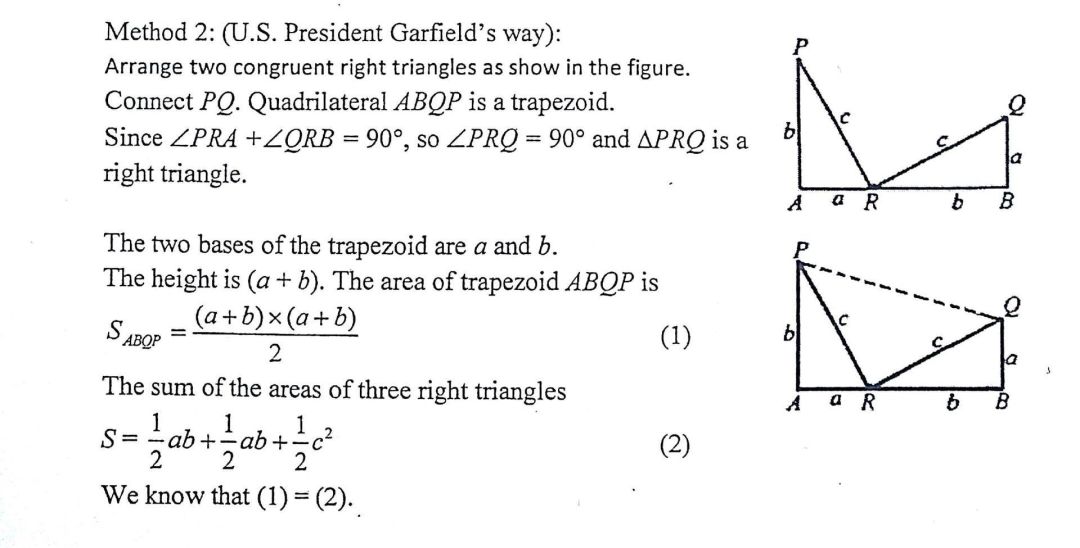
利用梯形面積就是三個三角形面積之和，知道兩式相等，然后解出這個式子↓↓

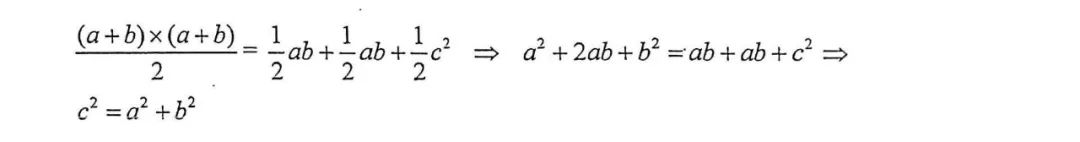
以上兩個證法都是基于面積，如果用一些較為現代的數學工具，比如相似三角形 (similar triangles) 那么證明過程就會縮短不少：

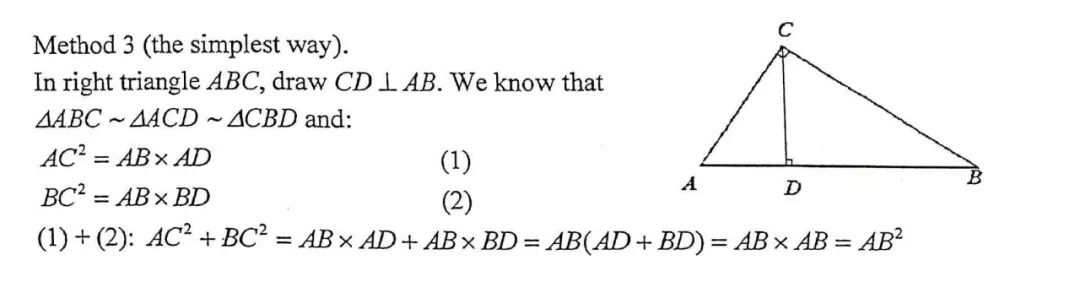
事實上，勾股定理目前有500多種證法，是證明方法最多的數學定理之一。

知道了勾股定理的來源和證明，下面我們來看看它的應用：

一個重要性質（上圖性質1）就是在直角三角形三邊上做三個相似的圖形，最大的圖形面積等于兩個小圖面積之和（如下圖右側三個例子），證明思路是：相似圖形面積比等于邊長比的平方，而邊長的平方之間的關系就是兩個小的加起來等于大的。

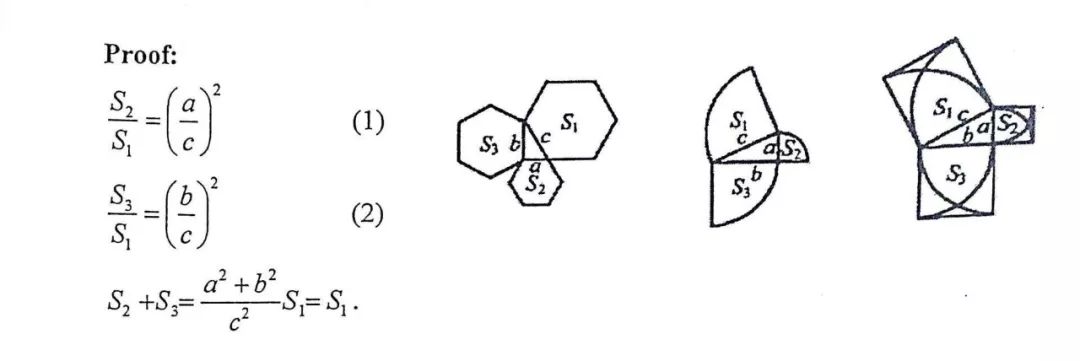
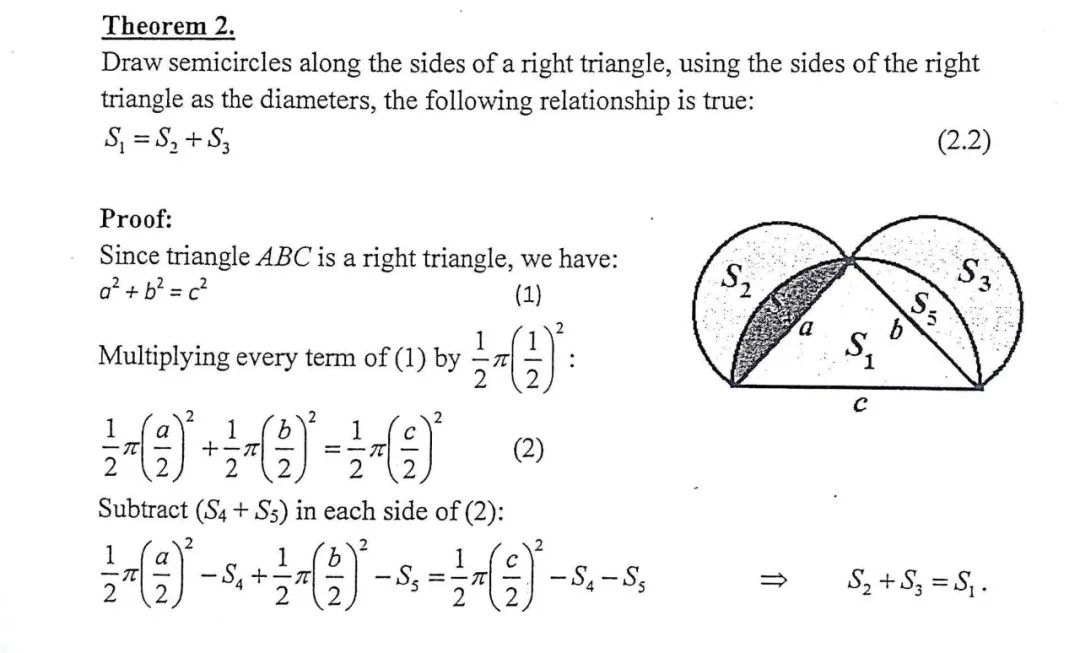
如果做的圖形是半圓，結合“直徑所對的圓周角是直角”，可推出：以斜邊為直徑向內做半圓，會經過直角頂點（如下圖）。再用面積做差，推出一個新的性質：兩個“月牙”面積之和等于三角形面積。

在前面的例子中，我們知道如果一個三角形是直角三角形，那么它的三邊 (a,b,c) 就滿足 a 方加 b 方等于 c 方，并且在實際題目中，常常出現 （3,4,5）/（6,8,10）/（5,12,13）這樣的 (a,b,c) ，這樣滿足勾股定理的整數，就叫“勾股數”（pythagorean triple) ,勾股數有兩個基本性質一：如果一組數是勾股數，那么它們的倍數依然是勾股數。比如 (3,4,5) 是勾股數，那么 (6,8,10) / (9,12,15) / (12,16,20) 以及 (300,400,500) 一定都滿足勾股定理，這些勾股數就構成了一類，即 (3k,4k,5k) 。

換個角度講，如果一組數中三個數可以約分，那么約分到互質 (relatively prime) 后的結果也是勾股數，而且這組勾股數是同類中最小的，這些已經互質的最小的勾股數叫做勾股方程的本原解。

（一部分本原解）二：所有的本原解可以被不重不漏地表示出。其實我們就是就是想知道 “a 方加 b 方等于 c 方”這個方程有哪些互質的 (a,b,c) 解。利用數論知識可以求出，所有互質的解是：

也就是說，有了這個表達式，任意選取兩個兩個符合條件的 m，n 就能立馬“生成”一組勾股數。更直觀來看，所有的勾股數，把兩直角邊的長度作為橫縱坐標（下圖是實軸坐標和虛軸坐標），就能把所有的勾股數畫在圖上，每組勾股數的（a，b，c）分別對應橫坐標、縱坐標、到原點的距離，這三個量都是整數。

好，今天你學習了《AMC系列》的第二講，了解了勾股定理的證明，也學會了它的用法和與代數的聯系。恭喜你，又解鎖了AMC數學學術活動的一個新章節。下次我們將學習學術活動中的相似三角形。