哪些學生有資格參加AIME？AIME難度如何?（附AIME真題及解析）

作為全球影響力最大，適配范圍最廣的數(shù)學學術活動，美國AMC學術活動被越來越多的家庭選擇并參加。在斯坦福、麻省理工、卡內基梅隆大學等美國頂尖學府申請中，AMC及AIME成績是學校衡量學生數(shù)學能力的指標之一，也是重要的升學籌碼。

想要拿下名校錄取，僅有AMC10/12已經(jīng)不夠了，晉級AIME并拿下重磅獎項才能提升競爭力！但別說拿獎，想要晉級AIME一點也不簡單！

什么是AIME？

AIME是美國數(shù)學邀請賽(American Invitational Mathematics Examination)的首字母縮寫，是美國數(shù)學學術活動AMC(American Mathematics Competition)系列賽事之一，也是美國國際數(shù)學奧林匹克(IMO)代表隊系列選拔賽的第二項賽事。

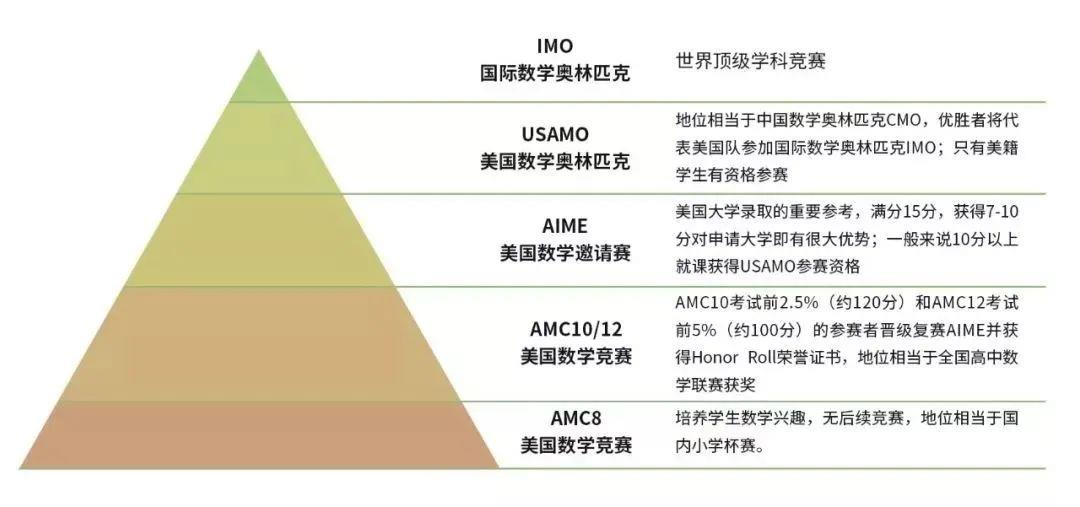絕大多數(shù)晉級AIME的選手是高中生，也有極少數(shù)頂尖的初中生可晉級AIME。從AMC 12晉級并在AIME中取得高分的選手將晉級USAMO，而從AMC 10晉級并在AIME中取得高分的選手將晉級USAJMO。

哪些學生有資格參加AIME？

AIME是邀請賽，在當年的AMC 10學術活動中排名前2.5%左右或AMC 12學術活動中排名前5%左右才能獲邀參賽。

AMC 10和12晉級AIME的分數(shù)線通常在考試前3周左右公布。

【AMC10歷年分數(shù)線】

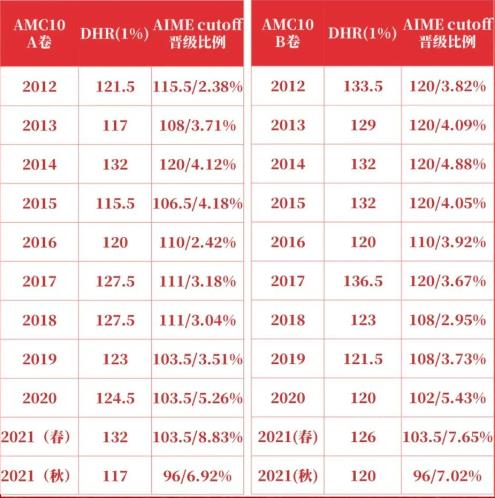
【AMC12歷年分數(shù)線】

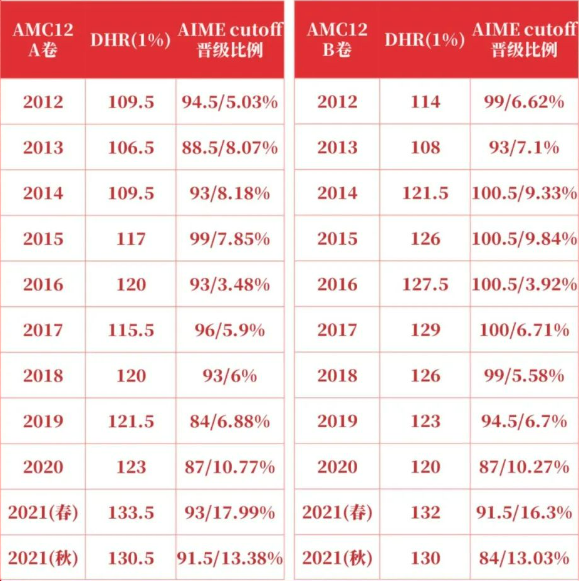
AIME?考試設置

【考試時長】：3小時

【考試日期】：AIME I: 2023年2月7日；AIME II: 2023年2月15日

【試卷語言】：中英雙語

【試卷構成】：15道填空題。需要注意的是，每道題答案的區(qū)間都只能是在000-999數(shù)字之間

【滿分】：15分

【計分方式】︰一題一分，答錯不扣分

【參與方式】：AIME 無需報名，AMC10/12 分數(shù)達到晉級線后即可獲組委會邀請參與。

【考查范圍】：AIME和AMC 10、AMC 12一樣，考查范圍仍然是算術、代數(shù)、計數(shù)、幾何、數(shù)論和概率（微積分不在數(shù)學學術活動考查范圍內），但允許使用微積分方法解題。

掃碼免費領取AIME歷年真題及答案

掃碼獲取【2022最新AMC10/12真題+答案+視頻解析】

AIME難度如何？

AIME是填空題，填空題比選擇題的難度更大，沒有一點點參考信息，除此之外AIME的圖形、計算更復雜，串聯(lián)的知識也多，對做題速度要求高等~

AIME學術活動通常前幾題難度大致相當于AMC 12的水平，而越往后題目難度越大。通常多數(shù)學生能做出第1-5題；到了第6-10題則是區(qū)分度最大的題，經(jīng)過專門的訓練、在AMC12或AMC10中排名前1%左右的選手一般能做對一部分題；而一般在考場上能做出第11-15題都是極其頂尖的選手。

AIME與AMC相比，在廣度和深度上AIME都是AMC的加強版，如果不去強化復習，大體上來說，AIME和AMC的分數(shù)可能會呈現(xiàn)如下的對應關系：

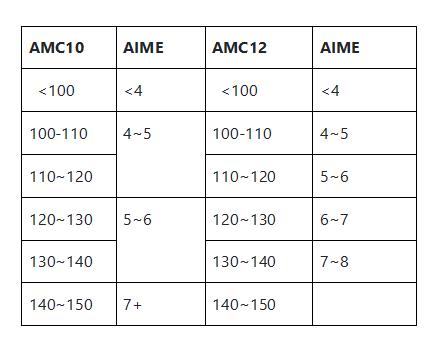
AIME學術活動真題及解析

因篇幅有限，僅展示部分真題

完整版真題及答案，可以添加【文中二維碼】免費領取~

---

翰林數(shù)學學術活動輔導課程火熱招生中！

班課和VIP（1V1）課程均已開放報名，歡迎掃文中二維碼聯(lián)系翰林顧問老師預約，先到先得。

AIME課程安排

開課測試和題目選講

1、進階代數(shù)第一部分 對數(shù)、三角函數(shù)、復數(shù)

2、進階代數(shù)第二部分 多項式、不等式、數(shù)列

3、方法論第一部分 不變性原理

真題測試解析

1、進階幾何第一部分 三角形、射影幾何

2、 進階幾何第二部分 圓、根軸

3、方法論第二部分 對稱性原理、幾何技巧

真題測試解析

1、進階數(shù)論第一部分 高次余數(shù)、費馬小定理、費馬-歐拉定理

2、進階數(shù)論第二部分 丟番圖方程

3、方法論第三部分 極限、構造方程

真題測試解析

1、進階排列組合第一部分 枚舉

2、 進階排列組合第二部分 遞推

3、 方法論第四部分 其他方法

真題測試解析

1、綜合第一部分

2、綜合第二部分

3、考前測試和考試注意事項

AMC8課程安排

1. Number theory

（1）Prime Factorizations

（2）Factors

（3）Base Number and Digits

2. Algebra

（1）Sequences and Series

（2）Special symbols and operations

（3）Ratios, Rates, and Proportions

（4）Functions

（5）Equation Inequations

(6) ?Sets and Venn Diagram

3. Geometry

（1）Angles and Polygons

（2）Triangles and Pythagorean

（3）Circles

（4）Volumes

4. Probability and Statistic

（1）Statistics

（2）Permutations and?Combinations

（3）Probability

（4）Logic and Reasoning